题目内容
【题目】在平面直角坐标系xOy中,给出如下定义:
对于⊙C及⊙C外一点P,M,N是⊙C上两点,当∠MPN最大时,称∠MPN为点P关于⊙C的“视角”.
(1)如图,⊙O的半径为1,
①已知点A(0,2),画出点A关于⊙O的“视角”;若点P在直线x=2上,则点P关于⊙O的最大“视角”的度数 ;
(2)在第一象限内有一点B(m,m),点B关于⊙O的“视角”为60°,求点B的坐标.
(3)若点P在直线y=﹣ ![]() x+2上,且点P关于⊙O的“视角”大于60°,求点P的横坐标xP的取值范围.
x+2上,且点P关于⊙O的“视角”大于60°,求点P的横坐标xP的取值范围.
(4)⊙C的圆心在x轴上,半径为1,点E的坐标为(0,1),点F的坐标为(0,﹣1),若线段EF上所有的点关于⊙C的“视角”都小于120°,直接写出点C的横坐标xC的取值范围.
【答案】
(1)60o
(2)解: ∵点B关于⊙O的视角为60°,
∴BM与⊙O相切,且∠MBO=30°,
∴点B在以O为圆心,2为半径的圆上,即OB=2,
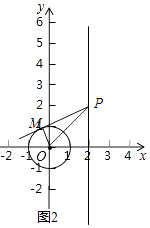
∵B(m,m) (m>0),
∴OB= ![]() =
= ![]() m=2,
m=2,
∴m= ![]()
∴B( ![]() ,
, ![]() );
);
(3)解: 如图3,
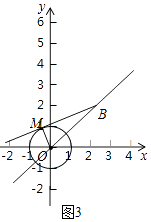
∵点P关于⊙O的“视角”大于60°,
∴∠MPO>30°,
∴sin∠MPO= ![]() >sin30°,
>sin30°,
∴OP<2,
∵点P不在⊙C上,
∴1<OP<2
∴点P在以O为圆心,1为半径与2为半径的圆环内,
∵点P在直线y= ![]() x+2上,
x+2上,
由图4,
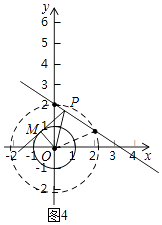
可得xp=0或xP= ![]()
∴0<xP< ![]()
(4)解: 如图5,

①当点C在x轴正半轴时,
在线段EF上取一点P,当PM,PN都与⊙C相切时,∠MPN最大,当∠MPN=120°时,连接CP,
∴∠CPM=60°,
在Rt△PCM中,CM=1,sin∠CPM= ![]() =
= ![]() =
= ![]() ,
,
∴CP= ![]() ,
,
∵线段EF上所有的点关于⊙C的“视角”都小于120°,
∴点P和原点O重合时,视角只要小于120°时,即可,OP最大=CP= ![]() ,
,
此时,满足条件的xC ![]()
②当点C在x轴负半轴时,同①可得,xC<﹣ ![]() ,
,
即:满足条件的xC ![]() 或xC<﹣
或xC<﹣ ![]()
【解析】(1)解: 画如图1所示,
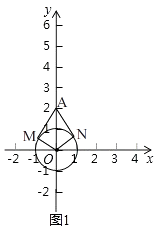
如图2,当∠MPN最大时,此时PM与PN与⊙O相切,
∵⊙O的半径为r=1,
∴sin∠MPO= ![]() ,
,
当OP最小时,此时sin∠MPO最大,即∠MPO最大,
∴sin∠MPO= ![]() ,
,
∴∠MPO=30°
∴∠MPN=2∠MPO=60°;

 字词句段篇系列答案
字词句段篇系列答案