题目内容
.如图,在矩形ABCD中,AB=5,BC=12,⊙O1和⊙O2分别是△ABC和△ADC的内切圆,则O1O2= .
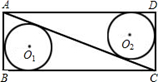

|
|
|
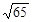
解析:∵矩形ABCD中,AB=5,BC=12;
∴AC=13,△ABC≌△CDA,则⊙O1和⊙O2的半径相等.
如图,过O1作AB、BC的垂线分别交AB、BC于N、E,过O2作BC、CD、AD的垂线分别交BC、CD、AD于F、G、H;
∵∠B=90°, ∴四边形O1NBE是正方形; 设圆的半径为r,根据切线长定理5-r+12-r=13,解得r=2, ∴BE=BN=2,
同理DG=HD=CF=2, ∴CG=FO2=3,EF=12-4=8;
过O1作O1M⊥FO2于M,则O1M=EF=8,FM=BN=2,
∴O2M=1, 在Rt△O1O2M中,O1O2=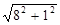 =
=![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
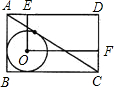 如图,在矩形ABCD中,连接AC,如果O为△ABC的内心,过O作OE⊥AD于E,作OF⊥CD于F,则矩形OFDE的面积与矩形ABCD的面积的比值为( )
如图,在矩形ABCD中,连接AC,如果O为△ABC的内心,过O作OE⊥AD于E,作OF⊥CD于F,则矩形OFDE的面积与矩形ABCD的面积的比值为( )A、
| ||
B、
| ||
C、
| ||
| D、不能确定 |
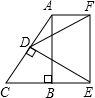 如图,在Rt△ABC中,∠ABC=90°,∠BAC=30°,点D是斜边AC上的中点,过点D作斜边AC的垂线,交CB的延长线于点E,将DE绕点D按逆时针方向旋转60°后得到线段DF,连接AF、EF.
如图,在Rt△ABC中,∠ABC=90°,∠BAC=30°,点D是斜边AC上的中点,过点D作斜边AC的垂线,交CB的延长线于点E,将DE绕点D按逆时针方向旋转60°后得到线段DF,连接AF、EF.