题目内容
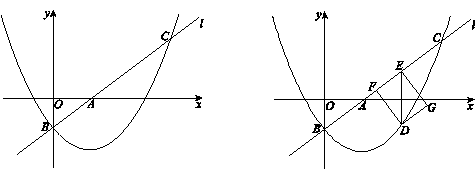
如图①，在矩形OABC中，OA=3，OC=4．将矩形OABC沿对角线AC剪开，再把△ABC向左平移3个单位，得到△A1B1C1（如图②），设A1C1交y轴于点E，B1C1交AC轴于点F．求点E、F的坐标．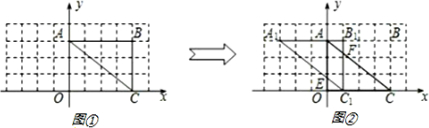
分析：由题意可得△A1AE∽△A1B1C1．即其对应边成比例，可依此求解AE的长，进而求出点E的坐标，再由平行线的性质可得点F的坐标．
解答：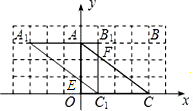
解：根据题意，得A（0，3）、B（4，3）、C（4，0）．
∵△ABC向左平移3个单位得到△A1B1C1，
∴A1（-3，3）、B1（1，3）、C1（1，0），AE∥B1C1．
∴△A1AE∽△A1B1C1．
∴
=
，AE=
=
=
．
∴OE=OA-AE=3-
=
．
∴点E的坐标为（0，
）．
∵AF∥C1E，AE∥FC1，
∴C1F=AE=
．
∴点F的坐标为（1，
）．
解：根据题意，得A（0，3）、B（4，3）、C（4，0）．∵△ABC向左平移3个单位得到△A1B1C1，
∴A1（-3，3）、B1（1，3）、C1（1，0），AE∥B1C1．
∴△A1AE∽△A1B1C1．
∴
| AE |
| A1B1 |
| A1A |
| A1B1 |
| A1A•B1C1 |
| A1B1 |
| 3×3 |
| 4 |
| 9 |
| 4 |
∴OE=OA-AE=3-
| 9 |
| 4 |
| 3 |
| 4 |
∴点E的坐标为（0，
| 3 |
| 4 |
∵AF∥C1E，AE∥FC1，
∴C1F=AE=
| 9 |
| 4 |
∴点F的坐标为（1，
| 9 |
| 4 |
点评：本题主要考查了相似三角形的判定及性质问题，其中涉及坐标与图形以及平移等的性质，能够掌握，并能够熟练运用．
练习册系列答案
通城学典默写能手系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
与
轴、
轴分别交于点A和点B(0，－1)，抛物线
经过点B，且与直线l的另一个交点为C(4，n)．
的值和抛物线的解析式： ;
