题目内容
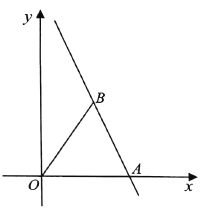
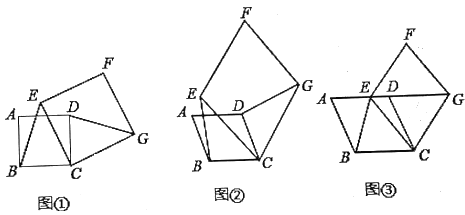
【题目】已知:如图,在四边形ABCD中,AB=3CD,AB∥CD,CE∥DA,DF∥CB.
(1)求证:四边形CDEF是平行四边形;
(2)填空:
①当四边形ABCD满足条件 时(仅需一个条件),四边形CDEF是矩形;
②当四边形ABCD满足条件 时(仅需一个条件),四边形CDEF是菱形.
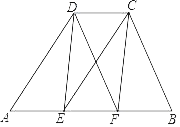
【答案】(1)详见解析;(2)①AD=BC;②AD⊥BC.
【解析】
(1)利用两组对边分别平行的四边形是平行四边形,可得四边形AECD和四边形BFDC都是平行四边形,再由一组对边平行且相等的四边形是平行四边形可得CDEF是平行四边形.(2)①当AD=BC时,四边形EFCD是矩形.理由是:对角线相等的平行四边形是矩形;②当AD⊥BC时,四边形EFCD是菱形.理由是:对角线互相垂直的平行四边形是菱形.
解:
(1)证明:∵AB∥CD,CE∥AD,DF∥BC,
∴四边形AECD和四边形BFDC都是平行四边形,
∴AE=CD=FB,
∵AB=3CD,
∴EF=CD,
∴四边形CDEF是平行四边形.
(2)解:①当AD=BC时,四边形EFCD是矩形.
理由:∵四边形AECD和四边形BFDC都是平行四边形,
∴EC=AD,DF=BC,
∴EC=DF,
∵四边形EFDC是平行四边形,
∴四边形EFDC是矩形.
②当AD⊥BC时,四边形EFCD是菱形.
理由:∵AD∥CE,DF∥CB,AD⊥BC,
∴DF⊥EC,
∵四边形EFCD是平行四边形,
∴四边形EFCD是菱形.
故答案为AD=BC,AD⊥BC.

练习册系列答案
相关题目