题目内容
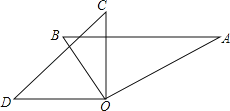
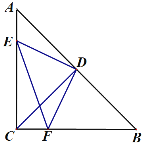
【题目】如图在△ABC中,∠ACB=90°,AC=BC,CD⊥AB于点D,点E、F分别在AC、BC上,且∠EDF=90°.
(1)求证:△AED≌△CFD;
(2)试判断CE、CF与CD之间的数量关系,并说明理由;
(3)若CF=1,CE=3,试求DF的长.
【答案】(1)证明见解析;(2)![]() ,理由见解析;(3)
,理由见解析;(3)![]() .
.
【解析】
(1)由等腰直角三角形的性质得到AD=BD=CD,∠A=∠B=∠DCF=45°.再由同角的余角相等得到∠ADE=∠CDF.用ASA即可证明△AED≌△CFD;
(2)由全等三角形的性质和等腰直角三角形的性质即可得出CE+CF=![]() AD;
AD;
(3)过D作DG⊥CA于G.由△AED≌△CDF可以求得AC、AD的长,再由等腰直角三角形的性质得出AG、DG的长,从而得到EG的长,再DF=ED和勾股定理即可得出结论.
(1)∵∠ACB=90°,AC=BC,∴△ABC是等腰直角三角形.
∵CD⊥AB,∴AD=BD=CD,∠A=∠B=∠DCF=45°.
∵∠EDF=90°,∴∠EDC+∠CDF=∠EDC+∠ADE=90°,∴∠ADE=∠CDF.
在△AED和△CDF中,∵ ∠ADE=∠CDF,AD=CD,∠A=∠DCF,∴△AED≌△CFD;
(2)∵△AED≌△CFD,∴AE=CF,∴CE+CF=CE+AE=AC.
∵△ADC是等腰直角三角形,∴AC=![]() AD,∴CE+CF=
AD,∴CE+CF=![]() AD;
AD;
(3)过D作DG⊥CA于G.由(2)得:△AED≌△CFD ,AC=CE+CF=4,CE+CF=![]() AD,∴ED=FD,3+1=
AD,∴ED=FD,3+1=![]() AD,解得:AD=
AD,解得:AD=![]() .
.
∵∠A=45°,∴△AGD是等腰直角三角形,∴AG=DG=2.
∵AE=CF=1,∴EG=AG-AE=2-1=1,∴DF=ED=![]() .
.


练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目