题目内容
已知点A,B分别是两条平行线m,n上任意两点,C是直线n上一点,且∠ABC=90°,点E在AC的延长线上,BC=kAB(k≠0).
(1)当k=1时,在图(1)中,作∠BEF=∠ABC,EF交直线m于点F.写出线段EF与EB的数量关系,并加以证明;
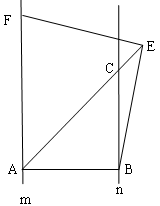
(2)若k≠1,如图(2),∠BEF=∠ABC,其它条件不变,探究线段EF与EB的数量关系,并说明理由.
(1)当k=1时,在图(1)中,作∠BEF=∠ABC,EF交直线m于点F.写出线段EF与EB的数量关系,并加以证明;

(2)若k≠1,如图(2),∠BEF=∠ABC,其它条件不变,探究线段EF与EB的数量关系,并说明理由.

(1) EF=EB;(2)EB=KEF
试题分析:(1)在直线m上截取AM=AB,连接ME,易证△MAE≌△BAE,则EM=EB,再根据等角对等边即可证明EM=EF,从而得到结果
(2)过点E作EM⊥m,可以证明四边形MENA为矩形,进而即可证明△MEF∽△NEB,根据相似三角形的对应边的比相等即可得到结果.
(1)在直线m上截取AM=AB,连接ME
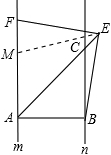
BC=kAB,k=1,
∴BC=AB,
∠ABC=90°,
∴∠CAB=∠ACB=45°,
∵m∥n,
∴∠MAE=∠ACB=∠CAB=45°,
∠FAB=90°,
∵AE=AE,
∴△MAE≌△BAE,
∴EM=EB,∠AME=∠ABE,
∵∠BEF=∠ABC=90°,
∴∠FAB+∠BEF=180°,
∴∠ABE+∠EFA=180°,
又∵∠AME+∠EMF=180°,
∴∠EMF=∠EFA,
∴EM=EF,
∴EF=EB;
(2)过点E作EM⊥m,EN⊥AB,垂足为M,N,
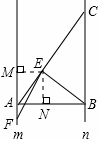
∴∠EMF=∠ENA=90°,
∵m∥n,∠ABC=90°,
∴∠MAB=90°,
∴四边形MENA为矩形,
∴ME=NA,∠MEN=90°,
∵∠BEF=∠ABC=90°,
∴∠MEF=∠NEB,
∴△MEF∽△NEB,
∴
 ,
,∴
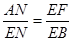
在Rt△ANE和Rt△ABC中,

∴EB=KEF.
点评:本题知识点多,综合性强,难度较大,正确作出辅助线是解题的关键.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
 ,那么称点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果
,那么称点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果 ,那么称直线l为该图形的黄金分割线.
,那么称直线l为该图形的黄金分割线.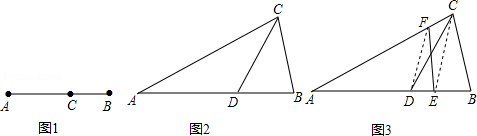
 ∽
∽ : .
: .
 .
. ,并说明理由。
,并说明理由。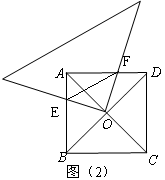
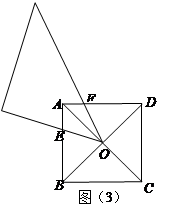
 ,求
,求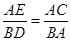 .
.
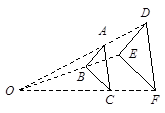

 成立吗?请说明理由.
成立吗?请说明理由.
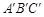 . 请在图中画出△
. 请在图中画出△ 的坐标;
的坐标;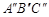 .
.