Question

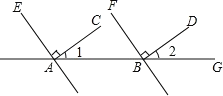
【题目】已知，BC∥OA，∠B＝∠A＝108°，试解答下列问题：

（1）如图1所示，则∠O＝　 　°，并判断OB与AC平行吗？为什么？

（2）如图2，若点E、F在线段BC上，且满足∠FOC＝∠AOC，并且OE平分∠BOF．则∠EOC的度数等于　 　°；

（3）在第（2）题的条件下，若平行移动AC，如图3．

①求∠OCB：∠OFB的值；

②当∠OEB＝∠OCA时，求∠OCA的度数（直接写出答案，不必写出解答过程）．

Answer 1

【答案】（1）72，OB∥AC，见解析；（2）40；（3）①∠OCB：∠OFB＝1：2；②∠OCA＝54°

【解析】

（1）首先根据平行线的性质可得∠B+∠O＝180，再根据∠A＝∠B可得∠A+∠O＝180，进而得到OB∥AC；

（2）根据角平分线的性质可得∠EOF＝∠BOF，∠FOC＝∠FOA，进而得到∠EOC＝（∠BOF+∠FOA）＝∠BOA＝40；

（3）①由BC∥OA可得∠FCO＝∠COA，进而得到∠FOC＝∠FCO，故∠OFB＝∠FOC+∠FCO＝2∠OCB，进而得到∠OCB：∠OFB＝1：2；

②由（1）知：OB∥AC，BC∥OA，得到∠OCA＝∠BOC，∠OEB＝∠EOA，根据（1）、（2）的结果求得．

解：（1）∵BC∥OA，∠B=108

∴∠O＝180-108=72，

∵BC∥OA，

∴∠B+∠O＝180，

∵∠A＝∠B

∴∠A+∠O＝180，

∴OB∥AC

故答案为：72；

（2）∵∠A＝∠B＝108，由（1）得∠BOA＝180﹣∠B＝72，

∵∠FOC＝∠AOC，并且OE平分∠BOF，

∴∠EOF＝∠BOF，∠FOC＝∠FOA，

∴∠EOC＝∠EOF+∠FOC＝（∠BOF+∠FOA）＝∠BOA＝36

故答案为：36；

（3）①∵BC∥OA，

∴∠FCO＝∠COA，

又∵∠FOC＝∠AOC，

∴∠FOC＝∠FCO，

∴∠OFB＝∠FOC+∠FCO＝2∠OCB，

∴∠OCB：∠OFB＝1：2；

②由（1）知：OB∥AC，∴∠OCA＝∠BOC，

由（2）可以设：∠BOE＝∠EOF＝α，∠FOC＝∠COA＝β，

∴∠OCA＝∠BOC＝2α+β

由（1）知：BC∥OA，

∴∠OEB＝∠EOA＝α+β+β＝α+2β

∵∠OEB＝∠OCA

∴2α+β＝α+2β

∴α＝β

∵∠AOB＝72，

∴α＝β＝18

∴∠OCA＝2α+β＝36+18＝54．