题目内容
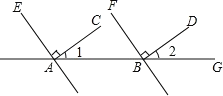
【题目】如图,已知AC⊥AE,BD⊥BF,∠1=35°,∠2=35°,AC与BD平行吗?AE与BF平行吗?
因为∠1=35°,∠2=35°(已知),所以∠1=∠2.所以___∥___( ).
又因为AC⊥AE(已知),所以∠EAC=90°( )
所以∠EAB=∠EAC+∠1=125°.
同理可得,∠FBG=∠FBD+∠2=__ °.
所以∠EAB=∠FBG( ).
所以___∥___(同位角相等,两直线平行).
【答案】AC;BD;同位角相等,两直线平行;垂直的定义;125;等量代换;AE;BF.
【解析】
根据同位角相等,两直线平行得到AC∥BD,根据垂直及等量代换得到∠EAB=∠FBG,根据同位角相等,两直线平行证明结论.
因为∠1=35°,∠2=35°(已知),
所以∠1=∠2.
所以AC∥BD(同位角相等,两直线平行).
又因为AC⊥AE(已知),
所以∠EAC=90°.(垂直的定义)
所以∠EAB=∠EAC+∠1=125°.
同理可得,∠FBG=∠FBD+∠2=125°.
所以∠EAB=∠FBG(等量代换).
所以AE∥BF(同位角相等,两直线平行).
故答案为:AC;BD;同位角相等,两直线平行;垂直的定义;125;等量代换;AE;BF.

练习册系列答案
相关题目