题目内容
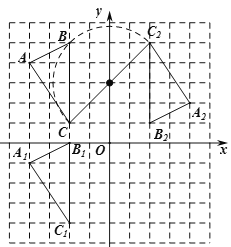
【题目】如图,![]() 在平面直角坐标系内,顶点的坐标分别为
在平面直角坐标系内,顶点的坐标分别为![]() ,
,![]() 、
、![]() .
.
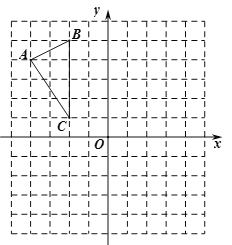
(1)平移![]() ,使点
,使点![]() 移到点
移到点![]() ,画出平移后的
,画出平移后的![]() ,并写出点
,并写出点![]() 的坐标.
的坐标.
(2)将![]() 绕点
绕点![]() 旋转
旋转![]() ,得到
,得到![]() ,画出旋转后的
,画出旋转后的![]() ,并写出点
,并写出点![]() 的坐标.
的坐标.
(3)求(2)中的点![]() 旋转到点
旋转到点![]() 时,点
时,点![]() 经过的路径长(结果保留
经过的路径长(结果保留![]() ).
).
【答案】(1)![]() ,见解析;(2)
,见解析;(2)![]() ,见解析;(3)
,见解析;(3)![]() .
.
【解析】
(1)根据点![]() 移到点
移到点![]() ,可得出平移的方向和距离,然后利用平移的性质分别求出点A1、B1的坐标即可解决问题;
,可得出平移的方向和距离,然后利用平移的性质分别求出点A1、B1的坐标即可解决问题;
(2)根据中心对称的性质,作出A、B、C的对应点A2、B2、C2,进一步即可解决问题;
(3)利用勾股定理计算CC2的长,再判断出点C经过的路径长是以CC2为直径的半圆,然后根据圆的周长公式计算即可.
解:解:(1)如图所示,则△A1B1C1为所求作的三角形,点A1的坐标是(﹣4,﹣1);
(2)如图所示,则△A2B2C2为所求作的三角形,点A2的坐标是(4,2);
(3)点C经过的路径长:是以(0,3)为圆心,以CC2为直径的半圆,由勾股定理得:CC2=![]() ,∴点C经过的路径长:
,∴点C经过的路径长:![]() ×π×
×π×![]() =2
=2![]() π.
π.

练习册系列答案
相关题目