题目内容
如图，在△ABC中，F、G是BC边上两点，使∠B、∠C的平分线BE、CD分别垂直AG，AF（E、D为垂足）．若△ABC的周长为22，BC边长为9，则DE的长为______．
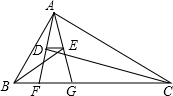
∵BE平分∠ABC，
∴∠ABE=∠GBE，
∵BE⊥AG，
∴∠AEB=∠GEB=90°，
∵BE=BE，
∴△GEB≌△AEB，
∴AB=BG，AE=EG，
同理AC=CF，AD=DF，
∴DE=
FG，
∵FG=BG+CF-BC，
=AC+AB-BC，
=（22-9）-9=4，
∴DE=2．
故答案为：2．
∴∠ABE=∠GBE，
∵BE⊥AG，
∴∠AEB=∠GEB=90°，
∵BE=BE，
∴△GEB≌△AEB，
∴AB=BG，AE=EG，
同理AC=CF，AD=DF，
∴DE=
| 1 |
| 2 |
∵FG=BG+CF-BC，
=AC+AB-BC，
=（22-9）-9=4，
∴DE=2．
故答案为：2．
练习册系列答案
应用题作业本系列答案
相关题目
