Question

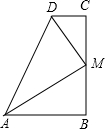
如图，在梯形ABCD中，∠C=90°，M是BC的中点，DM平分∠ADC，∠CMD=35°，则∠MAB是（　　）

A．35°

B．55°

C．70°

D．20°

Answer 1

∵∠C=90°，∠CMD=35°，
∴∠CDM=55°，
∵DM平分∠CDA，
∴∠CAD=2∠CDM=110°，
∵DC∥AB，
∴∠DAB=180°-∠CDA=70°，
过M作ME⊥AD于E，
∵∠C=90°，DM平分∠ADC，
∴ME=MC，
∵M为BC中点，
∴BM=MC，
∴ME=MB，
∵DC∥AB，∠C=90°，
∴∠B=90°，
∴∠EAM=∠BAM=

1

2

∠DAB=

1

2

×70°=35°，
故选A．