题目内容
【题目】如图,在平面直角坐标系xOy中,点A的坐标为(﹣2,0),等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD. 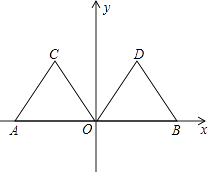
(1)△AOC沿x轴向右平移得到△OBD,则平移的距离是个单位长度;△AOC与△BOD关于直线对称,则对称轴是;△AOC绕原点O顺时针旋转得到△DOB,则旋转角度可以是度;
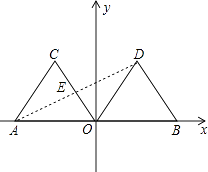
(2)连结AD,交OC于点E,求∠AEO的度数.
【答案】
(1)2;y轴;120
(2)解:如图,∵等边△AOC绕原点O顺时针旋转120°得到△DOB,
∴OA=OD,
∵∠AOC=∠BOD=60°,
∴∠DOC=60°,
即OE为等腰△AOD的顶角的平分线,
∴OE垂直平分AD,
∴∠AEO=90°.
故答案为2;y轴;120.
【解析】解:(1)∵点A的坐标为(﹣2,0), ∴△AOC沿x轴向右平移2个单位得到△OBD;
∴△AOC与△BOD关于y轴对称;
∵△AOC为等边三角形,
∴∠AOC=∠BOD=60°,
∴∠AOD=120°,
∴△AOC绕原点O顺时针旋转120°得到△DOB.
【考点精析】根据题目的已知条件,利用等边三角形的性质和轴对称的性质的相关知识可以得到问题的答案,需要掌握等边三角形的三个角都相等并且每个角都是60°;关于某条直线对称的两个图形是全等形;如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线;两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上.

练习册系列答案
相关题目