题目内容
【题目】如图，在
中， 
的中垂线
与的角平分线
交于点
，则四边形
的面积为____________
【答案】
【解析】
过点E作EG⊥AB交射线AB于G，作EH⊥AC于H，根据矩形的定义可得四边形AGEH为矩形，然后根据角平分线的性质可得EG=EH，从而证出四边形AGEH为正方形，可得AG=AH，然后利用HL证出Rt△EGB≌Rt△EHC，从而得出BG=HC，列出方程即可求出AG，然后根据S四边形ABEC= S四边形ABEH＋S△EHC即可证出S四边形ABEC= S正方形AGEH，最后根据正方形的面积公式求面积即可．
解：过点E作EG⊥AB交射线AB于G，作EH⊥AC于H
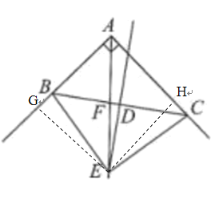
∴∠AGE=∠GAH=∠AHE=90°
∴四边形AGEH为矩形
∵AF平分∠BAC
∴EG=EH
∴四边形AGEH为正方形
∴AG=AH
∵DE垂直平分BC
∴EB=EC
在Rt△EGB和Rt△EHC中
∴Rt△EGB≌Rt△EHC
∴BG=HC
∴AG－AB=AC－AH
∴AG－3=4－AG
解得AG=
∴S四边形ABEC= S四边形ABEH＋S△EHC
= S四边形ABEH＋S△EGB
=S正方形AGEH
=AG2
=
故答案为：.
练习册系列答案
相关题目
