题目内容
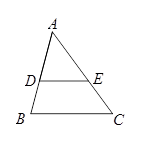
如图,在△ABC中,D、E分别是AB、AC上的点,且DE∥BC,若AD=5,DB=3,DE=4,则BC等于
A.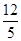 B.
B.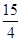 C.
C.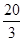 D.
D.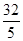

A.
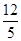 B.
B.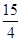 C.
C.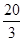 D.
D.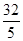
D.
试题分析:由AD=5,BD=3,即可求得AB=8,又由
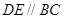 得:△ADE∽△ABC,根据相似三角形的对应边成比例,即可得
得:△ADE∽△ABC,根据相似三角形的对应边成比例,即可得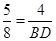 ,则可求得
,则可求得 .故选D.
.故选D.
练习册系列答案
相关题目
题目内容

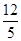 B.
B.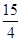 C.
C.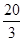 D.
D.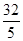
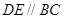 得:△ADE∽△ABC,根据相似三角形的对应边成比例,即可得
得:△ADE∽△ABC,根据相似三角形的对应边成比例,即可得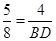 ,则可求得
,则可求得 .故选D.
.故选D.