题目内容
【题目】在平面直角坐标系中，点
，
，在坐标轴上取一点
，使
为等腰三角形，符合条件的点有（ ）
A.5个B.6个C.7个D.8个
【答案】B
【解析】
由A、B坐标可得AB=4，然后按A、B、C分别为顶点，即当AC=AB=4、BC=BA=4、CA=CB、画出图形，即可找到点C.
解：如图，∵
，
，∴AB=4
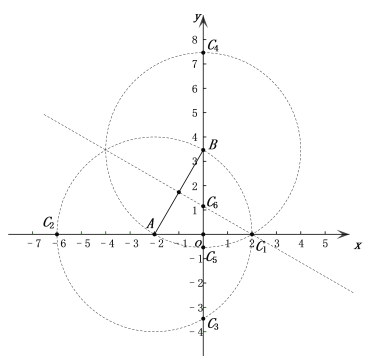
①当A为顶点时，即AC=AB=4，以A为圆心，以4为半径作圆交两轴于点C1，C2，C3，3个点；
②当B为顶点时，即BC=BA=4，以B为圆心，以4为半径作圆交两轴于点C4，C5， 2个点，与x正半轴的交点与C1重合；
③当C为顶点时，即CA=CB，作线段AB的垂直平分线交y轴于点C6，1个点，与x轴交点与C1重合.
所以符合条件的点
有6个.
故选：B
练习册系列答案
名校课堂系列答案
相关题目
