Question

在△ABC与△A′B′C′中，已知AB＜A′B′，BC＜B′C′，CA＜C′A′．下列结论：
（1）△ABC的边AB上的高小于△A′B′C′的边A′B′上的高；
（2）△ABC的面积小于△A′B′C′的面积；
（3）△ABC的外接圆半径小于△A′B′C′的外接圆半径；
（4）△ABC的内切圆半径小于△A′B′C′的内切圆半径．其中，正确结论的个数为（　　）

A．0

B．1

C．2

D．4

Answer 1

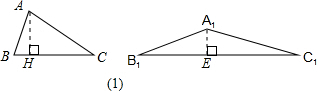
（1）如图所示在△ABC与△A′B′C′中，已知AB＜A′B′，BC＜B′C′，CA＜C′A′，但高AH＞A₁E，∴（1）错误；
（2）如上图，当高A₁E无限缩小时，△ABC的面积大于△A′B′C′的面积，∴（2）错误；
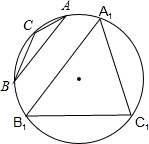
（3）如图a所示：△ABC和△A₁B₁C₁都是圆O的内接三角形，其外接圆的半径相等，∴（3）错误；
（4）作边长是5

3

的等边三角形ABC，可根据勾股定理求出其内切圆的半径是5，同样作此圆的外切直角三角形A₁B₁C₁，使三边长是6、8、10，符合已知条件，当两内切圆的半径相等，
（4）作边长是a的等边三角形ABC，另作顶角为120度的等腰三角形A1B1C1，满足已知条件，使两内切圆的半径相等，可知（4）错误．
故选A．