题目内容
如图，在△ABC与△ADE中，∠C=∠E，∠1=∠2，AC=AD=2AB=6，求AE的长．分析：由已知条件和相似三角形的判定方法证明△ABC∽ADE，利用相似三角形的性质：对应边的比值相等即可求出AE的长．
解答：解：∵∠1=∠2，
∴∠CAB=∠EAD，
∵∠C=∠E，
∴△ABC∽ADE，
∴
=
，
∵AC=AD=2AB=6，
∴
=
，
∴AE=12．
∴∠CAB=∠EAD，
∵∠C=∠E，
∴△ABC∽ADE，
∴
| AC |
| AE |
| AB |
| AD |
∵AC=AD=2AB=6，
∴
| 6 |
| AE |
| 3 |
| 6 |
∴AE=12．
点评：本题考查了相似三角形的判定和性质，是中考中常见的题型．
练习册系列答案
相关题目
34、如图，在△ABC与△EDF中，∠B=∠D=90°，∠A=∠E，B、F、C、D在一条直线上，添加一个条件
6、如图，在△ABC与△BCD中，AB=AC=4，BD交AC于E点，AE=3，且∠BAC=2∠BDC．则BE•ED=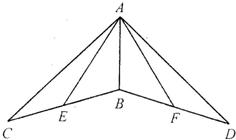
19、如图，在△ABC与△ABD中，BC=BD，∠ABC=∠ABD．点E为BC中点，点F为BD中点，连接AE，AF
如图，在△ABC与△DCB中，∠1=∠2，增加一个条件后，不能使△ABC≌△DCB的是（ ）
如图，在△ABC与△DCB中，∠A=∠D，要使△ABC≌△DCB，需要添加的一个条件是