��Ŀ����
����Ŀ������֪�߶�AB��ͬ����FAB����GBA������������AF��BG�Ϸֱ�ȡ��D��E�����߶�AB��ȡ��C������DC��EC��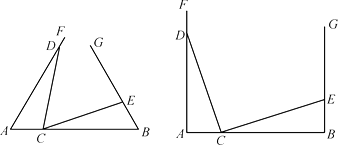
����ͼ����AD��3��BE��1����ADC�ա�BCE���ڡ�FAB����GBA��60���FAB����GBA��90�����������ѡһ�֣�����������⣺
���߶�AB�ij����Ƿ����仯��ֱ��д�����Ȼ�仯��Χ��
�ڡ�DCE�Ķ����Ƿ����仯��ֱ��д��������仯��Χ��
����AD��a��BE��b����FAB����GBA�������ҡ�ADC�͡�BCE������������ȫ�ȣ��������
���߶�AB�ij��Ȼ�ȡֵ��Χ����˵�����ɣ�
�ڡ�DCE�Ķ�����ȡֵ��Χ����˵�����ɣ�
���𰸡�ѡͼһ
��AB��4�����䣻
�ڡ�DCE��60.
��a ![]() bʱ����AB�� a��b�� �ڡ�DCE����
bʱ����AB�� a��b�� �ڡ�DCE����
��a=bʱ����AB��0. ��0����DCE��180.
ѡͼ��
�� AB��4�����䣻 �ڡ�DCE��90.
��a ![]() bʱ����AB�� a��b�� �ڡ�DCE����
bʱ����AB�� a��b�� �ڡ�DCE����
��a=bʱ���� AB��0. ��0����DCE��180.
��������ѡͼһ
�١ߡ�ADC�ա�BCE��
��BC=AD=3��AC=BE=1��
��AB=AC+BC=4��
��AB��4�����䣻
�ڡߡ�FAB����GBA��60��
���ADC+��ACD=120��
�ߡ�ADC�ա�BCE�����ADC=��BCE��
���BCE+��ACD=120��
���DCE��60.
��a ![]() bʱ�����ADC�ա�BCE��
bʱ�����ADC�ա�BCE��
�١ߡ�ADC�ա�BCE����BC=AD=a��AC=BE=b����AB�� a��b��
�ڡ�DCE����
��a=bʱ�����ADC�ա�BEC����AC=BC����
��AB��0. ��0����DCE��180.
ѡͼ��
�١ߡ�ADC�ա�BCE��
��BC=AD=3��AC=BE=1��
��AB=AC+BC=4��
��AB��4�����䣻
�ڡߡ�FAB����GBA��90��
���ADC+��ACD=90��
�ߡ�ADC�ա�BCE�����ADC=��BCE��
���BCE+��ACD=90��
���DCE��90.
��a ![]() bʱ�����ADC�ա�BCE��
bʱ�����ADC�ա�BCE��
�١ߡ�ADC�ա�BCE����BC=AD=a��AC=BE=b����AB�� a��b��
�ڡߡ�FAB����GBA������
���ADC+��ACD=180-����
�ߡ�ADC�ա�BCE�����ADC=��BCE��
���BCE+��ACD=180-����
���DCE������
��a=bʱ�����ADC�ա�BEC����AC=BC����
��AB��0. ��0����DCE��180.
���ݡ�ADC���BCE���Զ������Ӧ�ߣ�����֪��FAB����GBA������A��B��Ӧ��
�ڢ��У����ݡ�ADC�ա�BCE���õ���Ӧ����ȣ��ɵ��������õ�AB�ij������ݶ�Ӧ����ȡ��������ڽǺ���ƽ�ǵĶ������á�DCE��
�ڢ���Ҫ��D��C��Ӧ��D��E��Ӧ��������������ۣ��������������.

 ��Ӣ���㿨ϵ�д�
��Ӣ���㿨ϵ�д�