Question

【题目】如图，D为直角△ABC的斜边AB上一点，DE⊥AB交AC于E，如果△AED沿DE翻折，A恰好与B重合，联结CD交BE于F，如果AC═8，tanA═ ，那么CF：DF═

Answer 1

【答案】6：5
【解析】解：∵DE⊥AB，tanA═ ， ∴DE= AD，
∵Rt△ABC中，AC═8，tanA═ ，
∴BC=4，AB= =4 ，
又∵△AED沿DE翻折，A恰好与B重合，
∴AD=BD=2 ，DE= ，
∴Rt△ADE中，AE= =5，
∴CE=8﹣5=3，
∴Rt△BCE中，BE= =5，
如图，过点C作CG⊥BE于G，作DH⊥BE于H，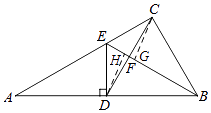

则Rt△BDE中，DH= =2，
Rt△BCE中，CG= = ，
∵CG∥DH，
∴△CFG∽△DFH，
∴ = = = ．
所以答案是：6：5．
【考点精析】根据题目的已知条件，利用翻折变换（折叠问题）和解直角三角形的相关知识可以得到问题的答案，需要掌握折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等；解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．