题目内容
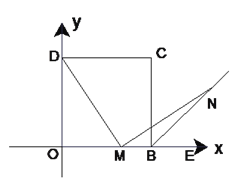
【题目】设点Q到图形W上每一个点的距离的最小值称为点Q到图形W的距离.例如正方形ABCD满足A(1,0),B(2,0),C(2,1),D(1,1),那么点O(0,0)到正方形ABCD的距离为1.
(1)如果⊙P是以(3,4)为圆心,1为半径的圆,那么点O(0,0)到⊙P的距离为
(2)求点 ![]() 到直线
到直线 ![]() 的距离;
的距离;
(3)如果点 ![]() 到直线
到直线 ![]() 的距离为3,求a的值.
的距离为3,求a的值.
【答案】
(1)4
(2)
解:直线 ![]() 记为
记为 ![]() ,过点
,过点 ![]() 作
作 ![]() ,垂足为点
,垂足为点 ![]() ,
,
设 ![]() 与
与 ![]() 轴的交点分别为
轴的交点分别为 ![]() ,则
,则 ![]() .
.
∴ ![]() .
.
∵ ![]()
∴ ![]() ,即
,即 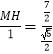 .∴
.∴ ![]() .
.
∴点 ![]() 到直线
到直线 ![]() 的距离为
的距离为 ![]() .
.
(3)
![]()
【解析】(1)OP=![]() =5,
=5,
点O(0,0)到⊙P的距离为5-1=4;
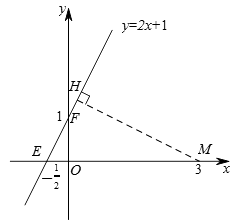
(2)直线 y = 2 x + 1 记为 l ,过点 M 作 M H ⊥ l ,垂足为点 H ,
设 ![]() 与
与 ![]() 轴的交点分别为
轴的交点分别为 ![]() ,则
,则 ![]() .
.
图1
∴ ![]() .
.
∵ ![]()
∴ ![]() ,即
,即 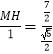 .∴
.∴ ![]() .
.
∴点 ![]() 到直线
到直线 ![]() 的距离为
的距离为 ![]() .
.
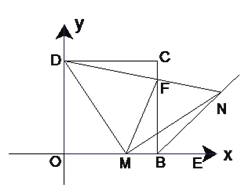
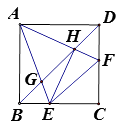
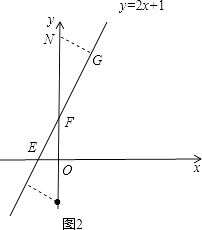
(3)②N在F点的上边,如图2,过点N作NG⊥l,垂足为点G,
∵△EOF∽△NGF,
∴![]() =
=![]() ,
,
即![]()
![]() ,
,
∴a=1+3![]() ;
;
N在F点的下边,
同理可得a=1-3![]() ;
;
故a=1±3![]() .
. 
(1)根据勾股定理可得点O(0,0)到⊙P的距离;
(2)过点M作MH⊥l,垂足为点H,通过证明△EOF∽△MHE,由相似三角形的性质可得MH , 从而得到点M到直线y=2x+1的距离;
(3)分两种情况:N在F点的上边;N在F点的下边;进行讨论先得到EN的长,进一步即可得到a的值.

【题目】在股市交易中,每买、卖一次需付交易款的千分之七点五作为交易费用,某投资者以每股10元的价格买入某股票1 000股,下表为第一周内每日该股票的涨跌情况(单位:元).
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 | +2 | +1.5 | -0.5 | -4.5 | +2.5 |
(1)星期三收盘时,每股是多少元?
(2)本周内每股最高价是多少元?最低价是多少元?
(3)若该投资者在星期五收盘前将股票全部卖出,他的收益情况如何?