题目内容
【题目】如图,平面直角坐标系xOy中,一次函数y=﹣x+b(b为常数,b>0)的图象与x轴、y轴分别交于A、B两点,半径为5的圆⊙O与x轴正半轴相交于点C,与y轴相交于D、E两点.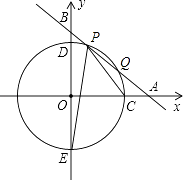
(1)若直线AB交劣弧 ![]() 于P、Q两点(异于C、D)
于P、Q两点(异于C、D)
①当P点坐标为(3,4)时,求b值;
②求∠CPE的度数,并用含b的代数式表示弦PQ的长(写出b的取值范围);
(2)当b=6时,线段AB上存在几个点F,使∠CFE=45°?请说明理由.
【答案】
(1)
解:①∵点P(3,4)在直线AB上,
∴﹣3+b=4,
∴b=7,②∵∠COE=90°,
∴∠CPE= ![]() ∠COE=45°,
∠COE=45°,
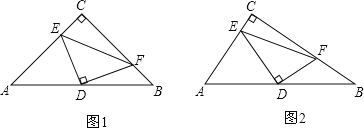
如图1,过点O作OM⊥AB于M,连接OP,

∵直线AB的解析式为y=﹣x+b①,
∴直线OM的解析式为y=x②,
联立①②解得点M( ![]() b,
b, ![]() b),
b),
∴OM2= ![]() b2,
b2,
在Rt△POM中,OP=5,根据勾股定理得,PM= ![]() =
= ![]() ,
,
∴PQ=2PM= ![]()
![]() ,
,
当点P和点D重合时,b=5
当OM=5时,b=﹣5 ![]() (舍)或b=5
(舍)或b=5 ![]() ,
,
∴5≤b<5 ![]() ,
,
即:PQ= ![]()
![]() (5≤b<5
(5≤b<5 ![]() )
)
(2)
解:当b=6时,线段AB上存在2个点F,使∠CFE=45°,
理由:由(1)②知,点F在劣弧 ![]() 上时,∠CFE=45°,
上时,∠CFE=45°,
由(1)②知,OM=5时,即:b=5 ![]() 时,直线AB与⊙O相切,
时,直线AB与⊙O相切,
当点B与点D重合时,b=5,
∴当b=6时,在5到5 ![]() 之间,
之间,
∴线段AB与⊙Q有两个交点,
即:当b=6时,线段AB上存在2个点F,使∠CFE=45°.
【解析】(1)①直接将点P的坐标代入直线y=﹣x+b中,即可求出b的值,②先求出直线OM的解析式,即可得出点M的坐标,进而得出OM,再用勾股定理即可得出PM,即可得出PQ;(2)先判断出点F是劣弧 ![]() 上时,∠CFE=45°,进而判断b=6是线段AB与⊙O的交点的个数即可得出结论.
上时,∠CFE=45°,进而判断b=6是线段AB与⊙O的交点的个数即可得出结论.