题目内容
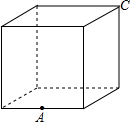 如图,是一个边长为2的正方体,现有一只蚂蚁要从一条棱的中点A处沿正方体的表面到C处,则它爬行的最短线路长是
如图,是一个边长为2的正方体,现有一只蚂蚁要从一条棱的中点A处沿正方体的表面到C处,则它爬行的最短线路长是
- A.5
- B.4
- C.

- D.

C
分析:将正方体沿棱长剪开,然后根据勾股定理求出蚂蚁爬行的路线的长度,再进行比较即可得解.
解答: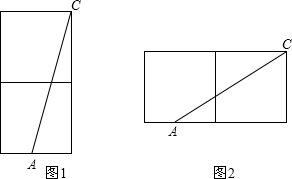 解:把正方体沿棱长剪开有两种展开图情况,
解:把正方体沿棱长剪开有两种展开图情况,
①如图1,∵正方体的棱长为2,点A为棱的中点,
∴直角三角形的两直角边分别为4、1,
∴AC= =
= ,
,
②如图2,∵正方体的棱长为2,点A为棱的中点,
∴直角三角形的两直角边分别为3、2,
∴AC=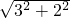 =
= ,
,
综上,它爬行的最短线路长是 .
.
故选C.
点评:本题考查平面展开最短路径问题,关键是知道两点之间线段最短,找到起点终点,根据勾股定理求出,注意展开情况有两种.
分析:将正方体沿棱长剪开,然后根据勾股定理求出蚂蚁爬行的路线的长度,再进行比较即可得解.
解答:
 解:把正方体沿棱长剪开有两种展开图情况,
解:把正方体沿棱长剪开有两种展开图情况,①如图1,∵正方体的棱长为2,点A为棱的中点,
∴直角三角形的两直角边分别为4、1,
∴AC=
 =
= ,
,②如图2,∵正方体的棱长为2,点A为棱的中点,
∴直角三角形的两直角边分别为3、2,
∴AC=
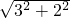 =
= ,
,综上,它爬行的最短线路长是
 .
.故选C.
点评:本题考查平面展开最短路径问题,关键是知道两点之间线段最短,找到起点终点,根据勾股定理求出,注意展开情况有两种.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 作图题:
作图题: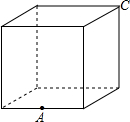 如图,是一个边长为2的正方体,现有一只蚂蚁要从一条棱的中点A处沿正方体的表面到C处,则它爬行的最短线路长是( )
如图,是一个边长为2的正方体,现有一只蚂蚁要从一条棱的中点A处沿正方体的表面到C处,则它爬行的最短线路长是( )