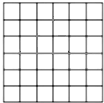
题目内容
作图题：如图，是一个边长为1的正方形网格，请在网格中画出一个边长为2
| 2 |
| 5 |
分析：关键是找出2
，
的长度，可利用勾股定理求出这些长度，从而画出三角形．
| 2 |
| 5 |
解答：解：2
看作是2、2为直角边的直角三角形的斜边．
可看作是以2和1为直角边的直角三角形的斜边，从而可画出三角形．
AB=2
，AC=
，BC=3．
△ABC符合要求．
| 2 |
| 5 |
AB=2
| 2 |
| 5 |
△ABC符合要求．
点评：本题考查勾股定理的应用，关键是用勾股定理求出斜边长，从而画出符合要求的三角形．
练习册系列答案
相关题目
作图题：如图，在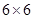
的正方形网格中，每个小正方形的边长都为1，请在所给网格中按下列要求画出图形．
|
；
（2）以（1）中的AB为边的一个等腰三角形ABC，使点C在格点上，且另两边的长都是无理数,请画出所有满足条件的点C；（3）画出△ABC关于点B的中心对称图形△A1B1C1。
作图题：如图，在
的正方形网格中，每个小正方形的边长都为1，请在所给网格中按下列要求画出图形．
|
；
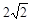（2）以（1）中的AB为边的一个等腰三角形ABC，使点C在格点上，且另两边的长都是无理数,请画出所有满足条件的点C；
（3）画出△ABC关于点B的中心对称图形△A1B1C1。
