��Ŀ����
ͬѧ�ǣ�ѧϰ��������֮�������Ѿ�����������������ʵ���ķ�Χ����˵�����ǵ�֪ʶԽ��Խ�ḻ�ˣ����ǣ�������������һ��ʲô�������أ������������ڼ��������ͼ������ʶһ����������
��1����ͼ�١�ABC��һ���߳�Ϊ2�ĵ���ֱ�������Σ����������2����������б�ߵĸ�����ƴ����ͼ�ڵ�������ABCD������������ε����Ҳ�͵��������ε������Ϊ2������������εı߳�����
������һ����������

��2����ͼ��ֱ��Ϊ1����λ���ȵ�Բ��ԭ��O���������ҹ���һ�ܣ�Բ�ϵ�һ��P������ʱ���O�غϣ���ԭ�㵽���O�䣬��OO��ij��Ⱦ͵���Բ���ܳ��У����������ϵ�O�������ʵ������

��3����ͼ����Rt��ABC�У���C=90�㣬AC=2��BC=1�����ݹ��ɶ��������AB=
������һ����������

���ˣ����Ŵ�Ҷ��������Dz������˸��������ʶ�ˣ���ô����Ҳ������ͼ�������������������ɣ�
1��������6��8������ͼ�У�ÿ��С�����α߳���Ϊ1��������һ����Ϊ
���߶���

2��ѧϰ��ʵ��������֪�������ϵĵ���ʵ����һһ��Ӧ�Ĺ�ϵ����ô�������������ҵ���ʾ -
�ĵ���

��1����ͼ�١�ABC��һ���߳�Ϊ2�ĵ���ֱ�������Σ����������2����������б�ߵĸ�����ƴ����ͼ�ڵ�������ABCD������������ε����Ҳ�͵��������ε������Ϊ2������������εı߳�����
| 2 |

��2����ͼ��ֱ��Ϊ1����λ���ȵ�Բ��ԭ��O���������ҹ���һ�ܣ�Բ�ϵ�һ��P������ʱ���O�غϣ���ԭ�㵽���O�䣬��OO��ij��Ⱦ͵���Բ���ܳ��У����������ϵ�O�������ʵ������
��
��
������һ����������
��3����ͼ����Rt��ABC�У���C=90�㣬AC=2��BC=1�����ݹ��ɶ��������AB=
| 5 |
| 5 |

���ˣ����Ŵ�Ҷ��������Dz������˸��������ʶ�ˣ���ô����Ҳ������ͼ�������������������ɣ�
1��������6��8������ͼ�У�ÿ��С�����α߳���Ϊ1��������һ����Ϊ
| 10 |

2��ѧϰ��ʵ��������֪�������ϵĵ���ʵ����һһ��Ӧ�Ĺ�ϵ����ô�������������ҵ���ʾ -
| 5 |

��������2���ɣ�1���������ǿ��Եõ������ϵ�O�������ʵ�������������У�
��3��ֱ�����ù��ɶ������AB���ɣ�
1������һ����Ϊ
���߶����⣬������֪ͼ�μ����ɶ����ó�������һ����ֱ�DZ�Ϊ3��1�������Σ���б�߳�Ϊ
��
2�����������ҵ���ʾ -
�ĵ�����(
)2=22+12������
Ӧ����ֱ�DZ�Ϊ2��1��ֱ�������ε�б�߳���
��3��ֱ�����ù��ɶ������AB���ɣ�
1������һ����Ϊ
| 10 |
| 10 |
2�����������ҵ���ʾ -
| 5 |
| 5 |
| 5 |
����⣺��2����OO��ij��Ⱦ͵���Բ���ܳ��У����������ϵ�O�������ʵ������ �У�
�ʴ�Ϊ�У�
��3����Rt��ABC�У���C=90�㣬AC=2��BC=1�����ݹ��ɶ����ã�
AB=
=
��
�ʴ�Ϊ��
��
�١�
=
��
�����ӽ�������3��С�����εĶԽ���AB����Խ���AB����Ҫ��һ����Ϊ
���߶���ͼ��
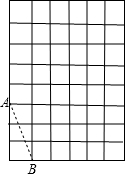
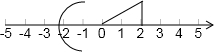
������������һ����ֱ�DZ߷ֱ�Ϊ2��1��ֱ�������Σ���ԭ��ΪԲ�ģ�����ֱ�DZߵ�б��Ϊ�뾶������������ĸ�������һ��A������������ı�ʾ-
�ĵ㣮
�ʴ�Ϊ�У�
��3����Rt��ABC�У���C=90�㣬AC=2��BC=1�����ݹ��ɶ����ã�
AB=
| 22+12 |
| 5 |
�ʴ�Ϊ��
| 5 |
�١�
| 10 |
| 32+12 |
�����ӽ�������3��С�����εĶԽ���AB����Խ���AB����Ҫ��һ����Ϊ
| 10 |

������������һ����ֱ�DZ߷ֱ�Ϊ2��1��ֱ�������Σ���ԭ��ΪԲ�ģ�����ֱ�DZߵ�б��Ϊ�뾶������������ĸ�������һ��A������������ı�ʾ-
| 5 |

���������⿼���֪ʶ����ʵ�������ᣬ�ؼ����ù��ɶ����������ʾ����������������Ҳ�����������ϱ�ʾ������һ��Ӧ��������Ϊֱ�DZ߳�Ϊ��������б�ߵij���

��ϰ��ϵ�д�
�����Ŀ
 ������һ����������
������һ����������
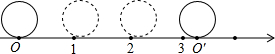

 ���߶���
���߶���
 �ĵ���
�ĵ���
 ������һ����������
������һ����������


 ���߶���
���߶���
 �ĵ���
�ĵ���