Question

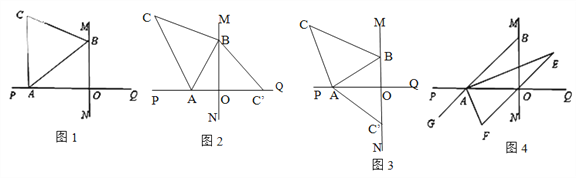
【题目】直线MN与直线PQ垂直相交于O，点A在射线OP上运动，点B 在射线OM上运动,A、B不与点O重合，如图1，已知AC、BC分别是∠BAP和∠ABM角的平分线，

（1）点A、B在运动的过程中，∠ACB的大小是否发生变化？若发生变化，请说明理由；若不发生变化，试求出∠ACB的大小.

（2）如图2，将△ABC沿直线AB折叠，若点C落在直线PQ上，则∠ABO＝________,

如图3，将△ABC沿直线AB折叠，若点C落在直线MN上，则∠ABO＝________

（3）如图4，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及其延长线交于E、F，则∠EAF＝ ；在△AEF中，如果有一个角是另一个角的倍，求∠ABO的度数.

Answer 1

【答案】（1）∠AEB的大小不会发生变化，∠AEB=135°；（2）30°，60°；（3）90°，60°或72°．

【解析】试题分析：(1)、根据角平分线的性质得出角度，然后根据三角形的内角和定理得出答案；(2)、根据角度之间的关系就可以分别进行计算，得出答案；(3)、根据角平分线的性质得出∠E=∠ABO和∠EAF=90°，然后根据直角三角形中角的关系求出∠E的度数，从而得出∠ABO的度数.

试题解析：(1)、∵AC、BC分别是∠BAP和∠ABM角的平分线

∴∠CAB=(180°-∠BAO)，∠CBA=(180°-∠ABO)

∴∠CAB+∠CBA=(180°-∠BAO +180°-∠ABO)=(360°-90°)=135°

∴∠ACB=180°-135°=45°，即∠ACB的大小不会改变，度数为45°.

(2)、30°，60°

(3)、∵∠BAO与∠BOQ的角平分线相交于E,

∴∠EAO= ∠BAO,∠EOQ=∠BOQ, ∴∠E=∠EOQ-∠EAO=（∠BOQ-∠BAO）=∠ABO,

∵AE、AF分别是∠BAO和∠OAG的角平分线, ∴∠EAF=90°．

在△AEF中,∵有一个角是另一个角的倍,故有：

①∠EAF=∠E,，∠E=60°,∠ABO=120°； ②∠EAF=∠F，∠E=30°，∠ABO=60°；

③∠F=∠E,∠E=36°,∠ABO=72°； ④∠E=∠F,∠E=54°,∠ABO=108°．

∴∠ABO为60°或72°．