题目内容
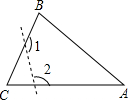
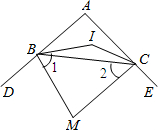
如图,△ABC中,∠A=100°,BI、CI分别平分∠ABC,∠ACB,则∠BIC=______,若BM、CM分别平分∠ABC,∠ACB的外角平分线,则∠M=______.

∵∠A=100°,
∵∠ABC+∠ACB=180°-100°=80°,
∵BI、CI分别平分∠ABC,∠ACB,
∴∠IBC=
∠ABC,∠ICB=
∠ACB,
∴∠IBC+∠ICB=
∠ABC+
∠ACB=
(∠ABC+∠ACB)=
×80°=40°,
∴∠I=180°-(∠IBC+∠ICB)=180°-40°=140°;
∵∠ABC+∠ACB=80°,
∴∠DBC+∠ECB=180°-∠ABC+180°-∠ACB=360°-(∠ABC+∠ACB)=360°-80°=280°,
∵BM、CM分别平分∠ABC,∠ACB的外角平分线,
∴∠1=
∠DBC,∠2=
ECB,
∴∠1+∠2=
×280°=140°,
∴∠M=180°-∠1-∠2=40°.
故答案为:140°;40°.
∵∠ABC+∠ACB=180°-100°=80°,
∵BI、CI分别平分∠ABC,∠ACB,
∴∠IBC=
| 1 |
| 2 |
| 1 |
| 2 |

∴∠IBC+∠ICB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠I=180°-(∠IBC+∠ICB)=180°-40°=140°;
∵∠ABC+∠ACB=80°,
∴∠DBC+∠ECB=180°-∠ABC+180°-∠ACB=360°-(∠ABC+∠ACB)=360°-80°=280°,
∵BM、CM分别平分∠ABC,∠ACB的外角平分线,
∴∠1=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠1+∠2=
| 1 |
| 2 |
∴∠M=180°-∠1-∠2=40°.
故答案为:140°;40°.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目