题目内容
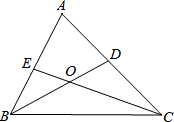
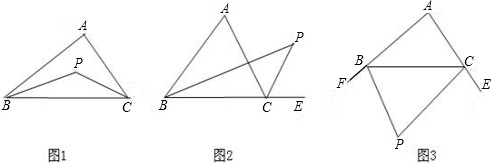
已知△ABC,(1)如图1,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°+
∠A;
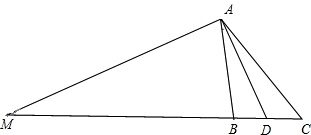
(2)如图2,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;
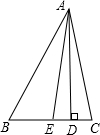
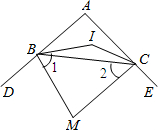
(3)如图3,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°-
∠A.
上述说法正确的个数是( )
| 1 |
| 2 |
(2)如图2,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;
(3)如图3,若P点是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°-
| 1 |
| 2 |
上述说法正确的个数是( )

| A.0个 | B.1个 | C.2个 | D.3个 |
(1)若P点是∠ABC和∠ACB的角平分线的交点,
则∠PBC=
∠ABC,∠PCB=
∠ACB
则∠PBC+∠PCB=
(∠ABC+∠ACB)=
(180°-∠A)
在△BCP中利用内角和定理得到:
∠P=180-(∠PBC+∠PCB)=180-
(180°-∠A)=90°+
∠A,
故成立;
(2)当△ABC是等腰直角三角形,∠A=90°时,结论不成立;
(3)若P点是外角∠CBF和∠BCE的角平分线的交点,
则∠PBC=
∠FBC=
(180°-∠ABC)=90°-
∠ABC,
∠BCP=
∠BCE=90°-
∠ACB
∴∠PBC+∠BCP=180°-
(∠ABC+∠ACB)
又∵∠ABC+∠ACB=180°-∠A
∴∠PBC+∠BCP=90°+
∠A,
在△BCP中利用内角和定理得到:
∠P=180-(∠PBC+∠PCB)=180-
(180°+∠A)=90°-
∠A,
故成立.
∴说法正确的个数是2个.
故选C.
则∠PBC=
| 1 |
| 2 |
| 1 |
| 2 |
则∠PBC+∠PCB=
| 1 |
| 2 |
| 1 |
| 2 |
在△BCP中利用内角和定理得到:
∠P=180-(∠PBC+∠PCB)=180-
| 1 |
| 2 |
| 1 |
| 2 |
故成立;
(2)当△ABC是等腰直角三角形,∠A=90°时,结论不成立;
(3)若P点是外角∠CBF和∠BCE的角平分线的交点,
则∠PBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∠BCP=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠PBC+∠BCP=180°-
| 1 |
| 2 |
又∵∠ABC+∠ACB=180°-∠A
∴∠PBC+∠BCP=90°+
| 1 |
| 2 |
在△BCP中利用内角和定理得到:
∠P=180-(∠PBC+∠PCB)=180-
| 1 |
| 2 |
| 1 |
| 2 |
故成立.
∴说法正确的个数是2个.
故选C.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目