题目内容
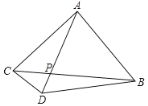
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 为
为![]() 中点,连接
中点,连接![]() ,
,![]() 于
于![]() ,交
,交![]() 于
于![]() ,连接
,连接![]() ,点
,点![]() 为
为![]() 中点,连接
中点,连接![]() ,以下结论:①
,以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 平分
平分![]() 。其中正确的结论的序号为___________。
。其中正确的结论的序号为___________。

【答案】③④
【解析】
作AP⊥AC交CE的延长线于P,连接CH.构造全等三角形,证明△CAP≌△BCG(ASA),△EAG≌△EAP(SAS),即可分步判断①②③,利用四点共圆可以证明④正确.
解:如图,作AP⊥AC交CE的延长线于P,连接CH.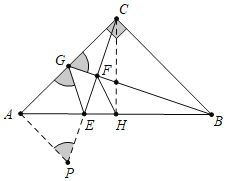
∵CE⊥BG,
∴∠CFB=∠ACB=90°,
∵∠ACE+∠BCE=90°,∠CBG+∠BCE=90°,
∴∠ACE=∠CBG,
∵BG是△ABC的中线,AB>BC,
∴∠ABG≠∠CBG,
∴∠ACE≠∠ABG,故①错误,
∵∠ACP=∠CBG,AC=BC,∠CAP=∠BCG=90°,
∴△CAP≌△BCG(ASA),
∴CG=PA=AG,∠BGC=∠P,
∵AG=AP,∠EAG=∠EAP=45°,AE=AE,
∴△EAG≌△EAP(SAS),
∴∠AGE=∠P,
∴∠AGE=∠CGB,故③正确,
∵![]() ,
,
∴△ABC是等腰直角三角形,
∴AC=BC=10,
∴AG=CG=5,
∴![]() ,
,
∵![]() ,
,
∴![]() ,故②错误,
,故②错误,
∵CA=CB,∠ACB=90°,AH=HB,
∴∠BCH=∠ACH=45°,
∵∠CFB=∠CHB=90°,
∴C,F,H,B四点共圆,
∴∠HFB=∠BCH=45°,
∴∠EFH=∠HFB=45°,
∴FH平分∠BFE,故④正确,
综上所述,正确的只有③④.
故答案为:③④

练习册系列答案
相关题目