题目内容
【题目】如图△ABC中,∠BAC=90°,AB=AC=AD,AD交BC于点P,∠CAD=30°,AC=6,求:
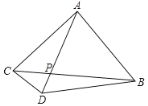
(1)∠BDC的度数,
(2)△ABD的周长
【答案】(1)1350(2)18
【解析】
(1)根据∠BAC=90°,∠CAD=30°可先求出∠DAB=60°,因为AB=AD,从而得出∠ADB的度数,之后利用AD=AC得出∠ADC度数,二者相加即可得出答案;
(2)由(1)可得△ABD是等边三角形,进而得出答案即可..
(1)∵∠BAC=90°,∠CAD=30°,
∴∠DAB=60°,
∵AD=AB,
∴△ABD是等边三角形,
∴∠ADB=60°,
又∵∠CAD=30°,AC=AD,
∴∠ADC=75°,
∴∠BDC=∠ADB+∠ADC=135°
(2)由(1)得△ABD是等边三角形,
∵AC=6,
∴AB=AD=BD=AC=6,
∴△ABD的周长为18.

练习册系列答案
相关题目









