题目内容
【题目】在平面直角坐标系xOy中,点A(t﹣1,1)与点B关于过点(t,0)且垂直于x轴的直线对称.
(1)以AB为底边作等腰三角形ABC,
①当t=2时,点B的坐标为 ;
②当t=0.5且直线AC经过原点O时,点C与x轴的距离为 ;
③若![]() 上所有点到y轴的距离都不小于1,则t的取值范围是 .
上所有点到y轴的距离都不小于1,则t的取值范围是 .
(2)以AB为斜边作等腰直角三角形ABD,直线m过点(0,b)且与x轴平行,若直线m上存在点P,![]() 上存在点K,满足PK=1,直接写出b的取值范围.
上存在点K,满足PK=1,直接写出b的取值范围.
【答案】(1)①(3,1);② 1;③ ![]() 或
或![]() ;(2)当点D在AB上方时,若直线m上存在点P,
;(2)当点D在AB上方时,若直线m上存在点P,![]() 上存在点K,满足PK=1,则
上存在点K,满足PK=1,则![]() ;当点D在AB下方时,若直线m上存在点P,
;当点D在AB下方时,若直线m上存在点P,![]() 上存在点K,满足PK=1,则
上存在点K,满足PK=1,则![]() .或
.或![]()
【解析】
(1)①根据A,B关于直线x=2对称解决问题即可.
②求出直线OA与直线x=0.5的交点C的坐标即可判断.
③由题意![]() ,根据△ABC上所有点到y轴的距离都不小于1,构建不等式即可解决问题.
,根据△ABC上所有点到y轴的距离都不小于1,构建不等式即可解决问题.
(2)由题意AB=![]() ,由△ABD是以AB为斜边的等腰直角三角形,推出点D到AB的距离为1,分两种情形分别求解即可解决问题.
,由△ABD是以AB为斜边的等腰直角三角形,推出点D到AB的距离为1,分两种情形分别求解即可解决问题.
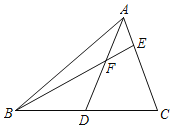
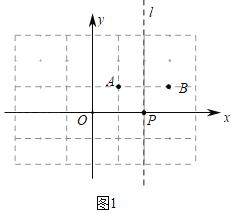
解:(1)①如图1中,
当![]()
![]()
![]() A(1,1),A,B关于直线x=2对称,
A(1,1),A,B关于直线x=2对称,
∴B(3,1).
故答案为(3,1).
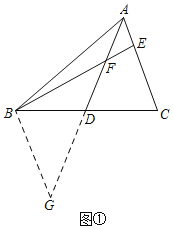
②如图2中,当![]()
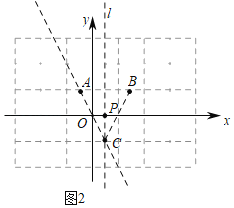
![]() A(﹣0.5,1),
A(﹣0.5,1),![]() ,直线l:x=0.5,
,直线l:x=0.5,
设![]() 为
为![]() ,
,
![]()
![]()
![]() 在
在![]() 上,
上,
![]() 直线AC的解析式为y=﹣2x,
直线AC的解析式为y=﹣2x,
∴C(0.5,﹣1),
∴点C到x轴的距离为1,
故答案为1.
③由题意![]() ,
,
∵![]() 上所有点到y轴的距离都不小于1,
上所有点到y轴的距离都不小于1,
∴t﹣1≥1或t+1≤﹣1,
解得![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.
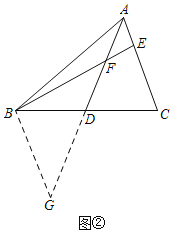
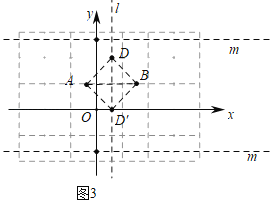
(2)如图3中,
∵![]() ,
,
∴AB=![]()
∵![]() 是以AB为斜边的等腰直角三角形,
是以AB为斜边的等腰直角三角形,
∴点D到AB的距离为1,
∴当点D在AB上方时,若直线m上存在点P,![]() 上存在点K,满足PK=1,则
上存在点K,满足PK=1,则![]() .
.
当点D在AB下方时,若直线m上存在点P,![]() 上存在点K,满足PK=1,则
上存在点K,满足PK=1,则![]() .
.
综上:![]() 的取值范围是:
的取值范围是:![]()