题目内容
【题目】阅读下面材料:
数学课上,老师给出了如下问题:
如图,AD为△ABC中线,点E在AC上,BE交AD于点F,AE=EF.求证:AC=BF.
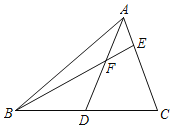
经过讨论,同学们得到以下两种思路:
思路一如图①,添加辅助线后依据SAS可证得△ADC≌△GDB,再利用AE=EF可以进一步证得∠G=∠FAE=∠AFE=∠BFG,从而证明结论.
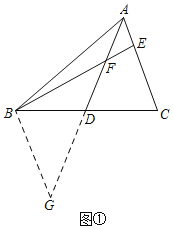
思路二如图②,添加辅助线后并利用AE=EF可证得∠G=∠BFG=∠AFE=∠FAE,再依据AAS可以进一步证得△ADC≌△GDB,从而证明结论.
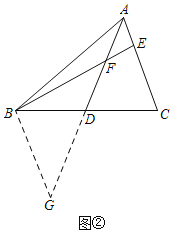
完成下面问题:
(1)①思路一的辅助线的作法是: ;
②思路二的辅助线的作法是: .
(2)请你给出一种不同于以上两种思路的证明方法(要求:只写出辅助线的作法,并画出相应的图形,不需要写出证明过程).
【答案】(1)①延长AD至点G,使DG=AD,连接BG;②作BG=BF交AD的延长线于点G;(2)详见解析
【解析】
(1)①依据SAS可证得△ADC≌△GDB,再利用AE=EF可以进一步证得∠G=∠FAE=∠AFE=∠BFG,从而证明结论.
②作BG=BF交AD的延长线于点G.利用AE=EF可证得∠G=∠BFG=∠AFE=∠FAE,再依据AAS可以进一步证得△ADC≌△GDB,从而证明结论.
(2)作BG∥AC交AD的延长线于G,证明△ADC≌△GDB(AAS),得出AC=BG,证出∠G=∠BFG,得出BG=BF,即可得出结论.
解:(1)①延长AD至点G,使DG=AD,连接BG,如图①,理由如下:
∵AD为△ABC中线,
∴BD=CD,
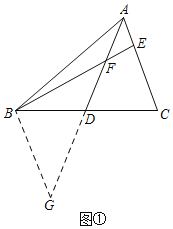
在△ADC和△GDB中,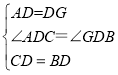 ,
,
∴△ADC≌△GDB(SAS),
∴AC=BG,
∵AE=EF,
∴∠CAD=∠EFA,
∵∠BFG=∠G,∠G=∠CAD,
∴∠G=∠BFG,
∴BG=BF,
∴AC=BF.
故答案为:延长AD至点G,使DG=AD,连接BG;
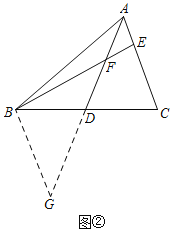
②作BG=BF交AD的延长线于点G,如图②.
理由如下:∵BG=BF,
∴∠G=∠BFG,
∵AE=EF,
∴∠EAF=∠EFA,
∵∠EFA=∠BFG,
∴∠G=∠EAF,
在△ADC和△GDB中,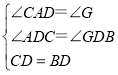 ,
,
∴△ADC≌△GDB(AAS),
∴AC=BG,
∴AC=BF;
故答案为:作BG=BF交AD的延长线于点G;
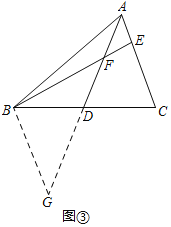
(2)作BG∥AC交AD的延长线于G,如图③所示:
则∠G=∠CAD,
∵AD为△ABC中线,
∴BD=CD,
在△ADC和△GDB中,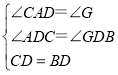 ,
,
∴△ADC≌△GDB(AAS),
∴AC=BG,
∵AE=EF,
∴∠CAD=∠EFA,
∵∠BFG=∠EFA,∠G=∠CAD,
∴∠G=∠BFG,
∴BG=BF,
∴AC=BF.

 阅读快车系列答案
阅读快车系列答案