题目内容
【题目】已知直线AB∥CD.
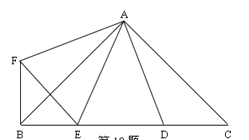
(1)如图1,直接写出∠ABE,∠CDE和∠BED之间的数量关系是 .
(2)如图2,BF,DF分别平分∠ABE,∠CDE,那么∠BFD和∠BED有怎样的数量关系?请说明理由.
(3)如图3,点E在直线BD的右侧,BF,DF仍平分∠ABE,∠CDE,请直接写出∠BFD和∠BED的数量关系 .

【答案】(1)∠ABE+∠CDE=∠BED;(2)详见解析;(3)2∠BFD+∠BED=360°.
【解析】试题分析:(1)点E作EF∥AB,根据平行线的性质易证得∠1=∠ABE,∠2=∠CDE,则可得∠ABE+∠CDE=∠BED;(2)∠BFD=![]() ∠BED,已知BF,DF分别平分∠ABE,∠CDE,根据角平分线的性质可得∠ABF=
∠BED,已知BF,DF分别平分∠ABE,∠CDE,根据角平分线的性质可得∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,所以∠ABF+∠CDF=
∠CDE,所以∠ABF+∠CDF=![]() ∠ABE+
∠ABE+![]() ∠CDE=
∠CDE=![]() (∠ABE+∠CDE),由(1)的结论可得∠BFD=∠ABF+∠CDF=
(∠ABE+∠CDE),由(1)的结论可得∠BFD=∠ABF+∠CDF=![]() (∠ABE+∠CDE),∠BED=∠ABE+∠CDE,所以∠BFD=
(∠ABE+∠CDE),∠BED=∠ABE+∠CDE,所以∠BFD=![]() ∠BED;(3过点E作EG∥CD,根据平行公理可得AB∥CD∥EG,根据平行线的性质易证∠ABE+∠CDE+∠BED=360°,再由(1)的方法可得∠BFD=∠ABF+∠CDF;已知BF,DF分别平分∠ABE,∠CDE,根据角平分线的性质可得∠ABF=
∠BED;(3过点E作EG∥CD,根据平行公理可得AB∥CD∥EG,根据平行线的性质易证∠ABE+∠CDE+∠BED=360°,再由(1)的方法可得∠BFD=∠ABF+∠CDF;已知BF,DF分别平分∠ABE,∠CDE,根据角平分线的性质可得∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,所以∠BFD=
∠CDE,所以∠BFD=![]() (∠ABE+∠CDE),即2∠BFD+∠BED=360°.
(∠ABE+∠CDE),即2∠BFD+∠BED=360°.
试题解析:
(1)∠ABE+∠CDE=∠BED.
理由:如图1,作EF∥AB,
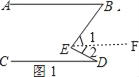
∵直线AB∥CD,
∴EF∥CD,
∴∠ABE=∠1,∠CDE=∠2,
∴∠ABE+∠CDE=∠1+∠2=∠BED,
即∠ABE+∠CDE=∠BED.
故答案为:∠ABE+∠CDE=∠BED.
(2)∠BFD=![]() ∠BED.
∠BED.
理由:如图2,∵BF,DF分别平分∠ABE,∠CDE,
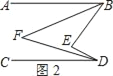
∴∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,
∠CDE,
∴∠ABF+∠CDF=![]() ∠ABE+
∠ABE+![]() ∠CDE=
∠CDE=![]() (∠ABE+∠CDE),
(∠ABE+∠CDE),
由(1),可得∠BFD=∠ABF+∠CDF=![]() (∠ABE+∠CDE)
(∠ABE+∠CDE)
∠BED=∠ABE+∠CDE,
∴∠BFD=![]() ∠BED.
∠BED.
(3)2∠BFD+∠BED=360°.
理由:如图3,过点E作EG∥CD,
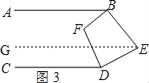
∵AB∥CD,EG∥CD,
∴AB∥CD∥EG,
∴∠ABE+∠BEG=180°,∠CDE+∠DEG=180°,
∴∠ABE+∠CDE+∠BED=360°,
由(1)知,∠BFD=∠ABF+∠CDF,
又∵BF,DF分别平分∠ABE,∠CDE,
∴∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,
∠CDE,
∴∠BFD=![]() (∠ABE+∠CDE),
(∠ABE+∠CDE),
∴2∠BFD+∠BED=360°.
故答案为:2∠BFD+∠BED=360°.