题目内容
如图,已知直线y=
x,点A的坐标是(4,0),点D为x轴上位于点A右边的某一点,点B为直线y=
x上的一点,以点A、B、D为顶点作正方形.
(1)若图①仅看作符合条件的一种情况,求出所有符合条件的点D的坐标;
(2)在图①中,若点P以每秒1个单位长度的速度沿直线y=
x从点O移动到点B,与此同时点Q以相同的速度从点A出发沿着折线A-B-C移动,当点P到达点B时两点停止运动.设点P运动时间为t,试探究:在移动过程中,△PAQ的面积关于t的函数关系式,并求最大值是多少?

| 3 |
| 4 |
| 3 |
| 4 |
(1)若图①仅看作符合条件的一种情况,求出所有符合条件的点D的坐标;
(2)在图①中,若点P以每秒1个单位长度的速度沿直线y=
| 3 |
| 4 |

(1)如图,



点D的坐标可以为(7,0)或(16,0)或(28,0);
(2)①当0<t≤3时,如图,过点P作PE⊥x轴,垂足为点E.
AQ=OP=t,OE=
t,AE=4-
t.
S△APQ=
AQ•AE=
t(4-
t)=-
(t-
)2+

当t=
时,S△APQ的最大值为
.
②当3<t≤5时,如图,
过点P作PE⊥x轴,垂足为点E,过点Q作QF⊥x轴,垂足为点F.
OP=t,PE=
t,OE=
t,AE=4-
t.
QF=3,AF=BQ=t-3,EF=AE+AF=1+
t
S△APQ=S梯形PEFQ-S△PEA-S△QFA
sAPQ=
t2-
t+6,由于对称轴为直线x=
,故当x=5时,S△APQ的最大值为3.
综上所述,S△APQ的最大值为3.



点D的坐标可以为(7,0)或(16,0)或(28,0);
(2)①当0<t≤3时,如图,过点P作PE⊥x轴,垂足为点E.
AQ=OP=t,OE=
| 4 |
| 5 |
| 4 |
| 5 |
S△APQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 5 |
| 2 |
| 5 |
| 5 |
| 2 |
| 5 |
| 2 |

当t=
| 5 |
| 2 |
| 5 |
| 2 |
②当3<t≤5时,如图,
过点P作PE⊥x轴,垂足为点E,过点Q作QF⊥x轴,垂足为点F.
OP=t,PE=
| 3 |
| 5 |
| 4 |
| 5 |
| 4 |
| 5 |
QF=3,AF=BQ=t-3,EF=AE+AF=1+
| 1 |
| 5 |
S△APQ=S梯形PEFQ-S△PEA-S△QFA
sAPQ=
| 3 |
| 10 |
| 21 |
| 10 |
| 7 |
| 2 |
综上所述,S△APQ的最大值为3.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目

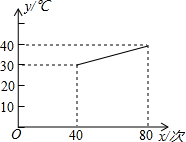
 >a)收费.设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图所示.
>a)收费.设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图所示.