题目内容
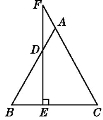
【题目】如图,∠B=∠C=36°,∠ADE=∠AED=72°,则图中的等腰三角形有( )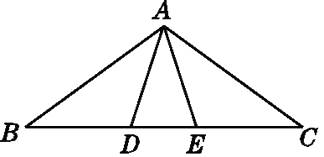
A.3个
B.4个
C.5个
D.6个
【答案】D
【解析】解:∵∠B=∠C=36°,∠ADE=∠AED=72°,∴△ABC和△ADE是等腰三角形,
∵∠B=36°,∠ADE=72°,
∴∠BAD=36°,
∴△ABD是等腰三角形,同理△AEC是等腰三角形,
∵∠ADE=∠AED=72°,
∴∠DAE=36°,
∴∠CAD=36°+36°=72°,
∴∠CAD=∠CDA=72°,
∴△ADC是等腰三角形,
同理:△ABE是等腰三角形,
综上所述:等腰三角形有6个,
故应选:D 。
根据有两个内角相等的三角形是等腰三角形得出△ABC和△ADE是等腰三角形;根据三角行的外角定理得出∠BAD=36°=∠B,从而得出△ABD是等腰三角形,同理△AEC是等腰三角形;根据三角形的内角和得出∠DAE=36°,根据角的和差得出∠CAD=36°+36°=72°,进而得出∠CAD=∠CDA=72°,故△ADC是等腰三角形,同理:△ABE是等腰三角形;从而得出结论。

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目