题目内容
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4)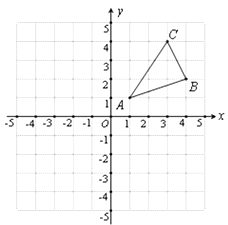
⑴ 作出与△ABC关于y轴对称△A1B1C1 , 并写出三个顶点的坐标为:A1(),B1(),C1();
【答案】-1,1;-4,2;-3,4
⑵ 在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标;
解:如图1,找出A的对称点A′(1,﹣1),连接BA′,与x轴交点即为P,点P坐标为(2,0);
⑶ 在 y 轴上是否存在点 Q,使得S△AOQ= ![]() S△ABC , 如果存在,求出点 Q 的坐标,如果不存在,说明理由。
S△ABC , 如果存在,求出点 Q 的坐标,如果不存在,说明理由。
解:设存在点 Q,使得S△AOQ= ![]() S△ABC , 如图2,作AD⊥y轴于D,设Q点坐标为(0,y),则 OQ=|y|,AD=1,
S△ABC , 如图2,作AD⊥y轴于D,设Q点坐标为(0,y),则 OQ=|y|,AD=1,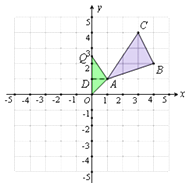
S△ABC= ![]() =
= ![]() ,
,
由题意,S△AOQ= ![]() S△ABC , 得
S△ABC , 得 ![]() ,
,![]() 或
或 ![]() ,
,
∴ Q点坐标为(0, ![]() )或(0,
)或(0, ![]() )
)
【解析】解:(1)△A1B1C1如图所示,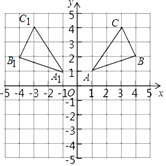
A1(-1,1),B1(-4,2),C1(-3,4);
故答案为:-1,1;-4,2;-3,4;
(1)根据关于y轴对称点的坐标特点可求出;
(2)找出A的对称点A′,连接BA′,与x轴交点即为P,从而得到P点的坐标;
(3)设存在点 Q,作AD⊥y轴于D,设Q点坐标为(0,y),则 OQ=|y|,AD=1.先求出△ABC的面积,从而可得△AOQ的面积,再由△AOQ的面积公式可求出y的值,即可得Q的坐标.

练习册系列答案
相关题目