Question

【题目】如图，在矩形中，对角线、交于点，将沿直线翻折，点落在点处，且，连接．求证：

（）是等边三角形．

（）．

Answer 1

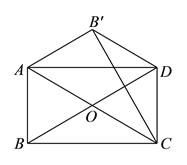
【答案】（1）证明见解析；（2）证明见解析.

【解析】试题分析：（1）由四边形ABCD是矩形，得到∠BAD=90°，AO=OD，得到∠OAD=∠ADO，根据平行线的性质得到∠B′AD=∠ADB，等量代换得到∠B′AD=∠DAC，根据折叠的性质得到∠BAC=∠CAB′，得到∠DAC=∠BAC，求得∠BAC=60°，于是得到结论；（2）连接B′O，推出B′C垂直平分OD，得到B′O=B′D，根据等腰三角形的性质得到∠OB′C=∠OCB′=30°，求得∠OCB′=∠CB′D，于是得到结论．

试题解析：（ ）∵四边形是矩形，

∴， ， ，

∴．

∵，

∴．

∵是由沿直线翻折得到，

∴，

∴，

∴，

∴．

∴是等边三角形．

（）∵是由沿直线翻折得到，

∴．

∵，

∴．

又，

∴四边形是平行四边形，

∴．