题目内容
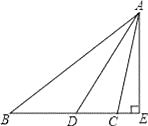
【题目】如图,在△ABC中,AB=AC,D是AB上的一点,过点D作DE⊥BC于E,并与CA的延长线交于点F.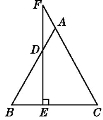
求证:△ADF是等腰三角形.
【答案】证明:∵DE⊥BC于E,
∴∠F+∠C=90°,∠B+∠BDE=90°.
∵∠FDA=∠BDE,
∴∠B+∠FDA=90°.
∴∠F+∠C=∠B+∠FDA.
∵ AB=AC,
∴∠B=∠C.
∴∠F=∠FAD ,
∴AF=AD,即△ADF是等腰三角形
【解析】根据直角三角形两锐角互余得出∠F+∠C=90°,∠B+∠BDE=90°,根据对顶角相等得出∠FDA=∠BDE,进而得出∠B+∠FDA=90° ,根据等边对等角得出∠B=∠C,根据等角的余角相等得出∠F=∠FAD ,根据两角相等的三角形是等腰三角形得出结论。

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目