题目内容
选做题:从甲乙两题中选作一题,如果两题都做,只以甲题计分
题甲:已知矩形两邻边的长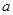 、
、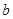 是方程
是方程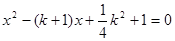 的两根.
的两根.
(1)求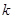 的取值范围;
的取值范围;
(2)当矩形的对角线长为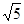 时,求
时,求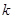 的值;
的值;
(3)当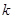 为何值时,矩形变为正方形?
为何值时,矩形变为正方形?
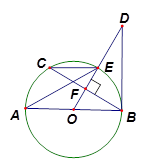
题乙:如图,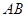 是
是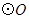 直径,
直径,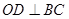 于点
于点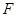 ,交
,交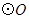 于
于
点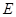 ,且
,且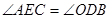 .
.
(1)判断直线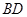 和
和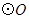 的位置关系,并给出证明;
的位置关系,并给出证明;
(2)当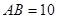 ,
,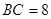 时,求
时,求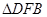 的面积.
的面积.
题甲:已知矩形两邻边的长
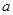 、
、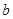 是方程
是方程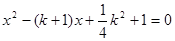 的两根.
的两根.(1)求
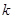 的取值范围;
的取值范围;(2)当矩形的对角线长为
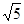 时,求
时,求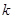 的值;
的值;(3)当
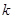 为何值时,矩形变为正方形?
为何值时,矩形变为正方形?
题乙:如图,
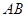 是
是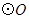 直径,
直径,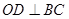 于点
于点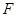 ,交
,交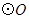 于
于点
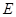 ,且
,且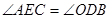 .
.(1)判断直线
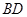 和
和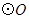 的位置关系,并给出证明;
的位置关系,并给出证明;(2)当
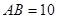 ,
,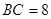 时,求
时,求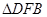 的面积.
的面积.题甲(1) (2)
(2) (3)
(3)
题乙:(1)BD是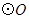 切线;证明
切线;证明 所以OB⊥BD,BD是
所以OB⊥BD,BD是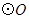 切线(2)S=
切线(2)S=
 (2)
(2) (3)
(3)
题乙:(1)BD是
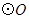 切线;证明
切线;证明 所以OB⊥BD,BD是
所以OB⊥BD,BD是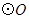 切线(2)S=
切线(2)S=
试题分析:题甲:(1)
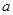 、
、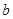 是方程
是方程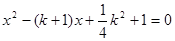 的两根,则其
的两根,则其 ;
;由
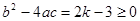 得
得
(2)矩形两邻边的长
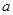 、
、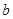 ,矩形的对角线的平方=
,矩形的对角线的平方= ;矩形两邻边的长
;矩形两邻边的长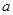 、
、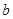 是方程
是方程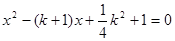 的两根,则
的两根,则 ;因为
;因为 ,所以
,所以 ;解得
;解得
由
 得
得
(3)矩形变为正方形,则a=b;
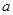 、
、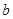 是方程
是方程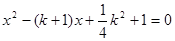 的两根,所以方程有两个相等的实数根,即
的两根,所以方程有两个相等的实数根,即 ,由
,由 得
得
题乙:(1)BD是切线;如图所示,
 是弧AC所对的圆周角,
是弧AC所对的圆周角, ;因为
;因为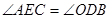 ,所以
,所以 ;
;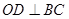 于点
于点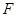 ,
, ,所以
,所以 ,
, ,在三角形OBD中
,在三角形OBD中 ,所以OB⊥BD;BD是
,所以OB⊥BD;BD是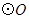 切线
切线(2)
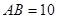 ,AB是圆的直径,所以OB=5;
,AB是圆的直径,所以OB=5;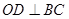 于点
于点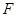 ,交
,交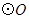 于
于点
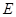 ,F是BC的中点;
,F是BC的中点;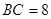 ,BF=4;在直角三角形OBF中由勾股定理得OF=
,BF=4;在直角三角形OBF中由勾股定理得OF= ;根据题意
;根据题意 ,
, ,则
,则 ,所以
,所以 ,从而
,从而 ,解得DF=
,解得DF= ,
,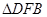 的面积=
的面积=
点评:本题考查直线与圆相切,相似三角形;解本题的关键是会判断直线与圆是否相切,能判定两个三角形相似

练习册系列答案
相关题目
 的圆形纸片中剪下40%圆周的 一个扇形,然后利用剪下的扇形制作成一个圆锥形玩具纸帽(接缝处不重叠),那么这个圆锥的高为
的圆形纸片中剪下40%圆周的 一个扇形,然后利用剪下的扇形制作成一个圆锥形玩具纸帽(接缝处不重叠),那么这个圆锥的高为



 ,求PA的长.
,求PA的长.
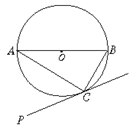
 .函数y=-x+2的图象与x轴交于点A,与y轴交于点B,点P为直线AB上一动点.
.函数y=-x+2的图象与x轴交于点A,与y轴交于点B,点P为直线AB上一动点.
