题目内容
【题目】已知:抛物线y=x2+(2m﹣1)x+m2﹣1经过坐标原点,且当x<0时,y随x的增大而减小.
(1)求抛物线的解析式;
(2)结合图象写出,0<x<4时,直接写出y的取值范围;
(3)设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB⊥x轴于点B,DC⊥x轴于点C.当BC=1时,求出矩形ABCD的周长.
【答案】
(1)
解:∵y=x2+(2m﹣1)x+m2﹣1经过坐标原点,
∴0=0+0+m2﹣1,即m2﹣1=0
解得m=±1.
又∵当x<0时,y随x的增大而减小,
∴m=﹣1,
∴二次函数解析式为y=x2﹣3x
(2)﹣ ![]() ≤y<4
≤y<4
(3)
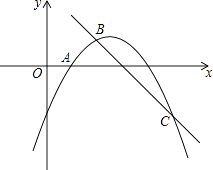
解:如图2中,
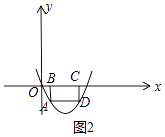
∵BC=1,B、C关于对称轴对称,
∴B(,1,0),C((2,0),
∵AB⊥x轴,DC⊥x轴,
∴A(1,﹣2),D(2,﹣2),
∴AB=DC=2,BC=AD=1,
∴四边形ABCD的周长为6,
当BC=1时,矩形的周长为6
【解析】解:(2)如图1中,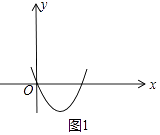
x=0时,y=0,
∵y=(x﹣ ![]() )2﹣
)2﹣ ![]() ,
,
∴x= ![]() 时,y最小值为﹣
时,y最小值为﹣ ![]() ,
,
x=4时,y=4,
∴0<x<4时,﹣ ![]() ≤y<4.
≤y<4.
所以答案是﹣ ![]() ≤y<4.
≤y<4.
【考点精析】通过灵活运用二次函数的图象,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点即可以解答此题.

练习册系列答案
相关题目