题目内容
 如图,在平行四边形ABCD中,E,F分别为边AB,CD的中点,BD⊥AD.
如图,在平行四边形ABCD中,E,F分别为边AB,CD的中点,BD⊥AD.
(1)求证:四边形BEDF是菱形;
(2)作AG⊥CB于G,若AD=1,AG=2,求sinC的值;
(3)若(2)中的四边形AGCD为一不可卷折的板材,问该板材能否通过一直径为1.8的圆洞门?请计算说明.
(1)证明:在平行四边形ABCD中,DC=AB,DC∥AB,
∴E,F分别是AB,CD的中点,
∴DF=BE,DF∥BE,
∴四边形BEDF是平行四边形,
又∵BD⊥AD,
所以DE= AB=BE,
AB=BE,
∴四边形BEDF是菱形;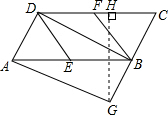
(2)解:由题意:DB⊥BC,
∴DB∥AC,又AD∥CG,
∴四边形AGBD是矩形,
∴DB=AG=2.
在平行四边形ABCD中,BC=AD=1,
∴CD=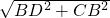 =
= ,
,
∴sinC=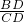 =
= =
= ;
;
(3)解:由(2)知,BG=AD=BC=1,
∴GC=2,
∴AG=GC=2>1.8,
作GH⊥CD于H.在直角△GCH中,GH=GC•sinC=2×
 ≈1.79<1.8,
≈1.79<1.8,
∴四边形能夹在平行于CD,且两者之间距离不足1.8的平行线之间.
∴该板材可以通过直径是1.8的圆洞口.
分析:(1)根据平行线的判定定理,证明对角线互相垂直的平行四边形是平行四边形是菱形,即可判断;
(2)首先可以证得:四边形AGBD是矩形,然后根据勾股定理即可求解;
(3)利用三角函数求得GH的长度,然后与1.8比较大小,即可判断.
点评:本题考查了平行四边形的性质,以及三角函数,正确求得CD的长是关键.
∴E,F分别是AB,CD的中点,
∴DF=BE,DF∥BE,
∴四边形BEDF是平行四边形,
又∵BD⊥AD,
所以DE=
 AB=BE,
AB=BE,∴四边形BEDF是菱形;

(2)解:由题意:DB⊥BC,
∴DB∥AC,又AD∥CG,
∴四边形AGBD是矩形,
∴DB=AG=2.
在平行四边形ABCD中,BC=AD=1,
∴CD=
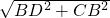 =
= ,
,∴sinC=
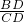 =
= =
= ;
;(3)解:由(2)知,BG=AD=BC=1,
∴GC=2,
∴AG=GC=2>1.8,
作GH⊥CD于H.在直角△GCH中,GH=GC•sinC=2×

 ≈1.79<1.8,
≈1.79<1.8,∴四边形能夹在平行于CD,且两者之间距离不足1.8的平行线之间.
∴该板材可以通过直径是1.8的圆洞口.
分析:(1)根据平行线的判定定理,证明对角线互相垂直的平行四边形是平行四边形是菱形,即可判断;
(2)首先可以证得:四边形AGBD是矩形,然后根据勾股定理即可求解;
(3)利用三角函数求得GH的长度,然后与1.8比较大小,即可判断.
点评:本题考查了平行四边形的性质,以及三角函数,正确求得CD的长是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在平行四边形ABCD中,AB=2
如图,在平行四边形ABCD中,AB=2| 2 |
| 3 |
| 5 |
| A、AC⊥BD |
| B、四边形ABCD是菱形 |
| C、△ABO≌△CBO |
| D、AC=BD |
 17、如图,在平行四边形ABCD中,EF∥AD,GH∥AB,EF、GH相交于点O,则图中共有
17、如图,在平行四边形ABCD中,EF∥AD,GH∥AB,EF、GH相交于点O,则图中共有 如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F,证明:四边形DFBE是平行四边形.
如图,在平行四边形ABCD中,∠ABC的平分线交CD于点E,∠ADC的平分线交AB于点F,证明:四边形DFBE是平行四边形. 的延长线交于点P,FP交AD于点Q.设运动时间为x秒,线段PC的长为y厘米.
的延长线交于点P,FP交AD于点Q.设运动时间为x秒,线段PC的长为y厘米. (2013•同安区一模)如图,在平行四边形ABCD中,已知∠ODA=90°,AC=10cm,BD=6cm,则AD的长为
(2013•同安区一模)如图,在平行四边形ABCD中,已知∠ODA=90°,AC=10cm,BD=6cm,则AD的长为