Question

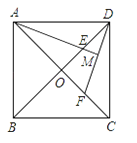
【题目】（8分）如图，在正方形ABCD中，对角线AC、BD相交于O，E、F分别在OD、OC上，且DE=CF，连结DF、AE，AE的延长线交于DF于点M，求证：AM⊥DF．

Answer 1

【答案】证明见试题解析．

【解析】

试题分析：根据DE=CF，可得出OE=OF，继而证明△AOE≌△DOF，得出∠OAE=∠ODF，然后利用等角代换可得出∠DME=90°，即得出了结论．

试题解析：∵四边形ABCD是正方形，∴CO=DO，又∵DE=CF，∴OD﹣DE=OC﹣CF，即OF=OE，在△AOE和△DOF中，∵AO=DO，∠AOD=∠DOF，OE=OF，∴△AOE≌△DOF（SAS），∴∠OAE=∠ODF，∵∠OAE+∠AEO=90°，∠AEO=∠DEM，∴∠ODF+∠DEM=90°，即可得AM⊥DF．