Question

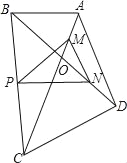
【题目】在△AOB中，AB=OB=2，△COD中，CD=OC=3，∠ABO=∠DCO．连接AD、BC，点M、N、P分别为OA、OD、BC的中点．

①若A、O、C三点在同一直线上，且∠ABO=2α，则 =_____（用含有α的式子表示）；

②固定△AOB，将△COD绕点O旋转，PM最大值为_____．

Answer 1

【答案】2sinα

【解析】

（1）连接BM、CN，则BM⊥OA，CN⊥OD，由四点共圆的判定知点B、C、M、N在以BC为直径的圆，且有MP=PN=BC÷2，而MN是△AOD的中位线，有MN等于AD的一半，故AD：BC=MN：PM，而可求得△PMN∽△BAO，有MN：PN=AO：AB=2sinα，从而求得AD：BC的值；

（2）取BO中点G，连接PG，MG，根据三角形中位线性质得PG=OC=，GM=AB=1，利用三角形三边的关系得PM≤GP+GM，所以当M，P，G共线的时候PM最大=1+1.5=2.5．

连接BM、CN．

∵AB=OB，M为OA的中点，∴BM⊥OA，∠AOB=∠COD=90°﹣α．同理CN⊥OD．

∵A、O、C三点在同一直线上，∴B、O、D三点也在同一直线上，∴∠BMC=∠CNB=90°．

∵P为BC中点，∴在Rt△BMC中，PM=BC．在Rt△BNC中，PN=BC，∴PM=PN，∴B、C、N、M四点都在以点P为圆心，BC为半径的圆上，∴∠MPN=2∠MBN．

又∵∠MBN=∠ABO=α，∴∠MPN=∠ABO，∴△PMN∽△BAO，∴，由题意知MN=AD，PM=BC，∴，∴．在Rt△BMA中，sinα．

∵AO=2AM，∴=2sinα，∴=2sinα；

（2）取BO中点G，连接PG，MG，则PG=OC=，GM=AB=1，利用三角形三边的关系得PM≤GP+GM，所以当M，P，G共线的时候PM最大=1+1.5=2.5．