题目内容
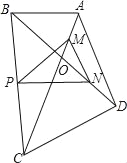
【题目】如图,![]() 和
和![]() 都是等边三角形,
都是等边三角形,![]() 和
和![]() 交于点
交于点![]() .
.

(1)求证:![]() ;
;
(2)下列结论中,正确的有________个.
①![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() 平分
平分![]() .
.
(3)请选择(2)中任一正确结论进行证明.你选的序号是 _________.
【答案】(1)见解析;(2)2个;(3)②或③;证明见解析
【解析】
(1)根据等边三角形的性质依据SAS可证得![]() ,从而证得绪论;
,从而证得绪论;
(2)根据(1)的结论以及等边三角形的性质可证得②③正确;
(3)选择②利用(2)的结论结合三角形内角和即可证得;选择③利用(2)的结论以及三角形面积结合角平分线的性质即可证得结论.
(1) ∵![]() 和
和![]() 都是等边三角形
都是等边三角形
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
即![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)如图,
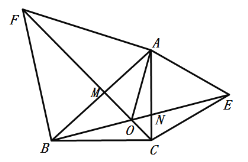
显然:①![]() ,故①错误;
,故①错误;
④![]() 不平分
不平分![]() ,故④错误;
,故④错误;
只有②和③是正确的,共2个;
故答案为:![]() 个;
个;
(3)选择②:∵![]()
∴![]()
又因为![]()
∴![]()
∴![]()
选择③:∵![]()
∴![]() ,
,![]()
过![]() 分别作
分别作![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,
,
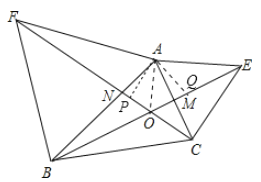
∴![]()
∴![]()
∴点![]() 在
在![]() 的平分线上
的平分线上
∴![]() 平分
平分![]()

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】二次函数y=ax2+bx+c (a、b、c为常数且a≠0)中的x与y的部分对应值如下表,
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 12 | 5 | 0 | -3 | -4 | -3 | 0 | 5 | 12 | … |
下列四个结论:
(1)二次函数y=ax2+bx+c 有最小值,最小值为-3;
(2)抛物线与y轴交点为(0,-3);
(3)二次函数y=ax2+bx+c 的图像对称轴是x=1;
(4)本题条件下,一元二次方程ax2+bx+c的解是x1=-1,x2=3.
其中正确结论的个数是( )
A. 4 B. 3 C. 2 D. 1