题目内容
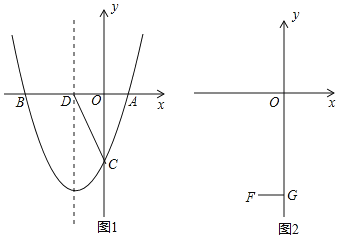
【题目】在平面直角坐标系![]() 中,四边形
中,四边形![]() 为正方形,点
为正方形,点![]() 的坐标为
的坐标为![]() ,动点
,动点![]() 沿边
沿边![]() 从
从![]() 向
向![]() 以每秒
以每秒![]() 的速度运动,同时动点
的速度运动,同时动点![]() 沿边
沿边![]() 从
从![]() 向
向![]() 以同样的速度运动,连接
以同样的速度运动,连接![]() 、
、![]() 交于点
交于点![]() .
.
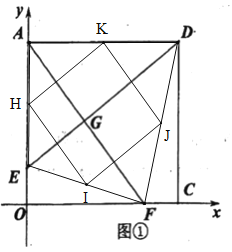
(1)试探索线段![]() 、
、![]() 的关系,写出你的结论并说明理由;
的关系,写出你的结论并说明理由;
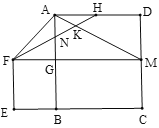
(2)连接![]() 、
、![]() ,分别取
,分别取![]() 、
、![]() 、
、![]() 、
、![]() 的中点
的中点![]() 、
、![]() 、
、![]() 、
、![]() ,则四边形
,则四边形![]() 是什么特殊平行四边形?请在图①中补全图形,并说明理由.
是什么特殊平行四边形?请在图①中补全图形,并说明理由.
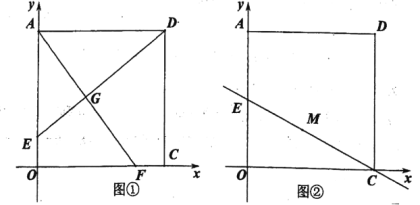
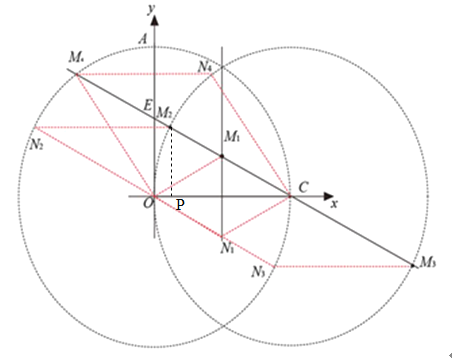
(3)如图②当点![]() 运动到
运动到![]() 中点时,点
中点时,点![]() 是直线
是直线![]() 上任意一点,点
上任意一点,点![]() 是平面内任意一点,是否存在点
是平面内任意一点,是否存在点![]() 使以
使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,请直接写出点
为顶点的四边形是菱形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)AF=DE,AF⊥DE,理由详见解析;(2)四边形HIJK为正方形,理由详见解析;(3)N的坐标为(2,-1),(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() ).
).
【解析】
(1)用SAS证明△DAE≌△AOF,根据全等三角形的性质得到DE=AF,∠ADE=∠OAF.根据等式的性质得到∠AGD=90°,从而得到AF⊥DE.
(2)根据三角形中位线定理得到IH=KJ=![]() AF,IH∥KJ,得到四边形HIJK为平行四边形,同理IJ=
AF,IH∥KJ,得到四边形HIJK为平行四边形,同理IJ=![]() DE,IJ∥DE,从而得到IJ=IH,IJ⊥IH,即可证明HIJK为正方形.
DE,IJ∥DE,从而得到IJ=IH,IJ⊥IH,即可证明HIJK为正方形.
(3)要求O、C、M、N四点构成菱形,OC为唯一已知线段,对OC的角色进行讨论:OC为对角线或OC为边.
当OC为对角线时,此时MN也为对角线,MN垂直平分OC,则M为OC中垂线与直线EC交点,可得M1的坐标,由对称可得此时N1的坐标.
当OC为边时,考虑M的位置,M与O相邻或者与C相邻.
Ⅰ.若M与C相邻,CM=CO=4,此时以C为圆心,OC长为半径作圆与直线EC交点即为M2和M3,过M2作M2P⊥OC于点P,得到OE∥PM2,即有△OEC∽△PM2C.根据相似三角形的对应边成比例,即可求出PM2,PC的长,进而得到OP的长.由N2M2∥OC,N2M2=OC,即可得到N2的坐标,由N3和N2关于原点对称,可得N3的坐标;
Ⅱ.若M与O相邻,OM=OC=4此时以O为圆心,OC长为半径作圆与直线EC交点即为M4.求出直线EC的解析式,则可得出M4的坐标,由OM4=4,解方程即可得出M4的坐标,从而得出N4的坐标.
(1)AF=DE,AF⊥DE.理由如下:
∵E、F速度相等,∴AE=OF.
∵OADC是正方形,∴AD=OA,∠DAE=∠AOF=90°,∴△DAE≌△AOF(SAS),∴DE=AF,∠ADE=∠OAF.
∵∠OAF+∠DAF=90°,∴∠ADE+∠DAF=90°,∴∠AGD=90°,∴AF⊥DE,∴AF=DE,AF⊥DE.
(2)四边形HIJK为正方形.理由如下:
由(1)知:AF=DE,AF⊥DE.
∵HI是△AEF的中位线、JK是△AFD的中位线,∴IH=![]() AF,IH∥AF,KJ=
AF,IH∥AF,KJ=![]() AF,KJ∥AF,∴IH=KJ,IH∥KJ,∴四边形HIJK为平行四边形,同理IJ=
AF,KJ∥AF,∴IH=KJ,IH∥KJ,∴四边形HIJK为平行四边形,同理IJ=![]() DE,IJ∥DE.
DE,IJ∥DE.
∵AF=DE,AF⊥DE,∴IJ=IH,IJ⊥IH,∴四边形HIJK为正方形.
(3)N的坐标为(2,-1),(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() ).
).
要求O、C、M、N四点构成菱形,OC为唯一已知线段,对OC的角色进行讨论:OC为对角线或OC为边.
当OC为对角线时,此时MN也为对角线,MN垂直平分OC,则M为OC中垂线与直线EC交点,可得M1(2,1)由对称可得此时N1(2,-1).
②当OC为边时,考虑M的位置,M与O相邻或者与C相邻.
Ⅰ.若M与C相邻,CM=CO=4,此时以C为圆心,OC长为半径作圆与直线EC交点即为M2和M3,过M2作M2P⊥OC于点P,∴OE∥PM2,∴△OEC∽△PM2C.
∵OE=2,OC=4,∴EC=![]() .
.
∵△OEC∽△PM2C,∴![]() ,∴
,∴![]() ,解得:PM2=
,解得:PM2=![]() ,PC=
,PC=![]() ,∴OP=OC-PC=
,∴OP=OC-PC=![]() .
.
∵N2M2∥OC,N2M2=OC,∴N2(![]() ,
,![]() ),易证N3和N2关于原点对称,∴N3(
),易证N3和N2关于原点对称,∴N3(![]() ,
,![]() ).
).
Ⅱ.若M与O相邻,OM=OC=4此时以O为圆心,OC长为半径作圆与直线EC交点即为M4.
设直线EC为y=kx+b,∴![]() ,解得:
,解得: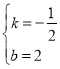 ,∴直线EC为
,∴直线EC为![]() .
.
设M4(x,![]() ),则
),则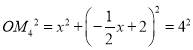 ,解得:
,解得:![]() ,
,![]() ,∴M4(
,∴M4(![]() ,
,![]() ),∴N4(
),∴N4(![]() ,
,![]() ).
).
综上所述:N的坐标为(2,-1),(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(
),(![]() ,
,![]() ).
).

 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案【题目】诗词是我国古代文化中的瑰宝,某市教育主管部门为了解本市初中生对诗词的学习情况,举办了一次“中华诗词”背诵大赛,随机抽取了部分同学的成绩(x为整数,总分100分),绘制了如下尚不完整的统计图表.
组别 | 成绩分组(单位:分) | 频数 |
A | 50≤x<60 | 40 |
B | 60≤x<70 | a |
C | 70≤x<80 | 90 |
D | 80≤x<90 | b |
E | 90≤x<100 | 100 |
合计 | c |
根据以上信息解答下列问题:
(1)统计表中a= ,b= ,c= ;
(2)扇形统计图中,m的值为 ,“E”所对应的圆心角的度数是 (度);
(3)若参加本次大赛的同学共有4000人,请你估计成绩在80分及以上的学生大约有多少人?