��Ŀ����
����Ŀ����1�����������֣�
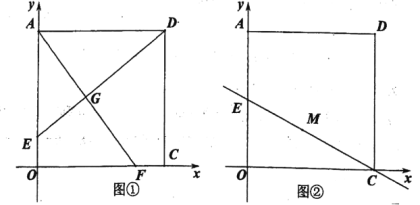
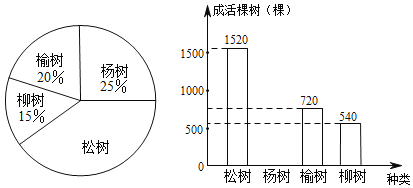
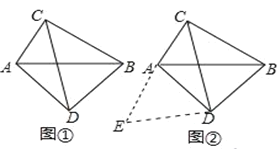
��ͼ1������ABC�Ƶ�A˳ʱ����ת50�㣬�õ���ADE������BD�����ABD���� ���ȣ�
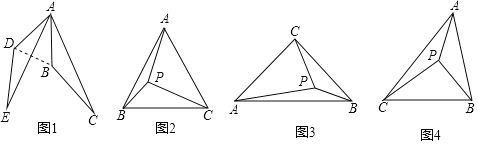
��2����������⣩
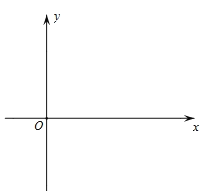
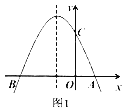
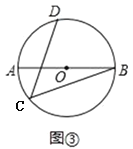
����ͼ2���ڱ߳�Ϊ![]() �ĵȱ�������ABC����һ��P����APC��90�㣬��BPC��120�㣬���APC�������
�ĵȱ�������ABC����һ��P����APC��90�㣬��BPC��120�㣬���APC�������
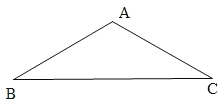
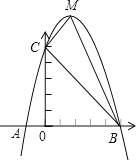
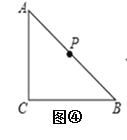
����ͼ3���ڡ�ABC�У���ACB��90�㣬AC��BC��P�ǡ�ABC�ڵ�һ�㣬��PB��1��PA��3����BPC��135�㣬��PC���� ����
��3������չӦ�ã�
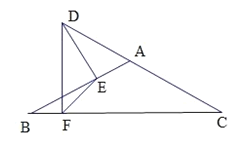
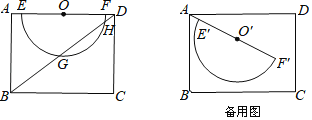
��ͼ4��A��B��C��������λ�õ�ƽ��ͼ��������AB��4��BC��3![]() ����ABC��75�㣬PΪ��ABC�ڵ�һ�����㣬����PA��PB��PC����PA+PB+PC����Сֵ��
����ABC��75�㣬PΪ��ABC�ڵ�һ�����㣬����PA��PB��PC����PA+PB+PC����Сֵ��
���𰸡���1��65����2����![]() ����2����3��PA+PB+PC����СֵΪ
����2����3��PA+PB+PC����СֵΪ![]() ��
��
��������
��1�����������֡�����ͼ1�У�������ת�����ʿɵ�AD��AB���ɵȱ߶ԵȽǺ��������ڽǺͶ���������𰸣�
��2����������⡿
����ͼ2�У�����APB�Ƶ�A����ʱ�뷽����ת60�㣬�õ���AP��C�䣬ֻҪ֤����PP��C��90�㣬���ù��ɶ������ɽ�����⣻
����ͼ3�У�����CBP���ŵ�C��˳ʱ�뷽����ת90�㣬�õ���CAP�䣬������ת�����ʿ��Եõ���P��CP����ACB��90�㣬�����õ�����ֱ�������Σ����PP'���ɵó��𰸣�
��3������չӦ�á�
��ͼ4�У�����APB��BC˳ʱ����ת60�㣬�õ���EDB������PD��CE���ó���CBE��135�㣬����E��EF��CB��CB���ӳ����ڵ�F�����CF��EF�ij��������CE������𰸿������
��1�����������֡�
�⣺��ͼ1�У�
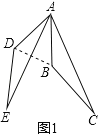
�ߡ�ABC�Ƶ�A˳ʱ����ת50�㣬�õ���ADE��
��AD��AB����DAB��50�㣬
��![]() ��65�㣬
��65�㣬
�ʴ�Ϊ��65��
��2����������⡿
���⣺��ͼ2�У��߽���APB�Ƶ�A����ʱ�뷽����ת60�㣬�õ���AP��C�䣬
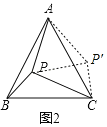
���APP���ǵȱ������Σ���AP��C����APB��360�㩁90�㩁120�㣽150�㣬
��PP�䣽AP����AP��P����APP�䣽60�㣬
���PP��C��90�㣬��P��PC��30�㣬
��PP�䣽![]() PC����AP��
PC����AP��![]() PC��
PC��
�ߡ�APC��90�㣬
��AP2+PC2��AC2������![]() PC��2+PC2����
PC��2+PC2����![]() ��2��
��2��
��PC��2��
��AP��![]() ��
��
��S��APC��![]() APPC��
APPC��![]() ��
��![]() ��2��
��2��![]() ��
��
����ͼ3������CBP���ŵ�C��˳ʱ�뷽����ת90�㣬�õ���CAP�䣬
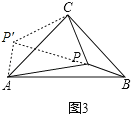
��CP�䣽CP����P��CP����ACB��90�㣬
���P��CPΪ����ֱ�������Σ�
���CP'P��45�㣬
�ߡ�BPC��135�㣽��AP'C��
���AP��P��90�㣬
��PA��3��PB��1��
��AP�䣽1��
��PP�䣽![]() ��
��![]() ��2
��2![]() ��
��
��PC��![]() ��
��![]() ��2��
��2��
�ʴ�Ϊ��2��
��3������չӦ�á�
�⣺��ͼ4�У�����APB��B˳ʱ����ת60�㣬�õ���EDB������PD��CE��
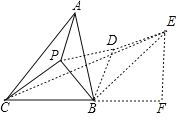
�߽���APB��B˳ʱ����ת60�㣬�õ���EDB��
���ABP����EBD��AB��EB��4����PBD��60�㣬��BPDΪ�ȱ������Σ�AP=DE
����ABP+��PBC����EBD+��PBC��PB=PD
����EBD+��PBC����ABC��75������������֮���߶���̿ɵ�PA+PB+PC=DE��PD��PC��CE����PA+PB+PC����СֵΪCE�ij�
����CBE��135����
����E��EF��CB��CB���ӳ����ڵ�F��
���EBF��45�㣬
��![]() ��
��
��Rt��CFE�У��ߡ�CFE��90�㣬BC��3![]() ��EF��2
��EF��2![]() ��
��
��![]() ��
��![]()
��PA+PB+PC����СֵΪ![]() ��
��