题目内容
已知四边形ABCD,对角线AC与BD互相垂直. 顺次连接其四条边的中点,得到新四边形的形状一定是( ).
| A.梯形 | B.矩形 | C.菱形 | D.正方形 |
B
试题分析:根据四边形对角线互相垂直,运用三角形中位线平行于第三边证明四个角都是直角,判断是矩形.

∵E、F、G、H分别为各边中点
∴EF∥GH∥DB,EF=GH=
 DB
DBEH=FG=
 AC,EH∥FG∥AC
AC,EH∥FG∥AC∵DB⊥AC
∴EF⊥EH
∴四边形EFGH是矩形.
故选B.
点评:解题时,主要是利用了三角形中位线定理的性质,比较简单,也可以利用三角形的相似,得出正确结论.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
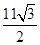
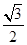
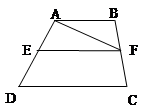
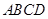 的对角线
的对角线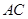 、
、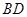 的长分别为12cm、16cm,
的长分别为12cm、16cm,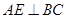 于点
于点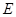 ,则
,则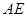 的长是_________cm.
的长是_________cm.

 倍,则这个多边形的边数是
倍,则这个多边形的边数是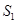 ;将图(1)中正方形边长增加2得到如图⑶所示的新正方形,此正方形的面积为
;将图(1)中正方形边长增加2得到如图⑶所示的新正方形,此正方形的面积为