��Ŀ����
֪ʶ������ͬѧ���Ѿ�ѧ���������Ĵ�С�Ƚϣ���ô��������ʽ��αȽϴ�С�أ�����ͨ��������Ƚϴ���ʽ��С�����磺��֪M=2x+3,N=2x+1���Ƚ�M��N�Ĵ�С������M��N����M��N>0����M>N����M��N<0����M<N����M��N=0����M=N����������ΪM��N=2>0������M>N��
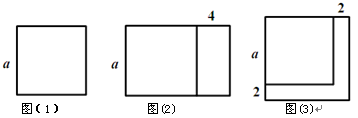
֪ʶӦ�ã�ͼ���DZ߳�Ϊa�������Σ���������һ�߲��䣬��һ������4���õ���ͼ����ʾ���³����Σ��˳����ε����Ϊ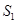 ����ͼ��1���������α߳�����2�õ���ͼ����ʾ���������Σ��������ε����Ϊ
����ͼ��1���������α߳�����2�õ���ͼ����ʾ���������Σ��������ε����Ϊ
���ú�a�Ĵ���ʽ��ʾ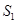 ��
�� ����Ҫ����
����Ҫ����
������������Ƚ� ��
�� ��С
��С
֪ʶӦ�ã�ͼ���DZ߳�Ϊa�������Σ���������һ�߲��䣬��һ������4���õ���ͼ����ʾ���³����Σ��˳����ε����Ϊ
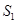 ����ͼ��1���������α߳�����2�õ���ͼ����ʾ���������Σ��������ε����Ϊ
����ͼ��1���������α߳�����2�õ���ͼ����ʾ���������Σ��������ε����Ϊ

���ú�a�Ĵ���ʽ��ʾ
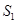 ��
�� ����Ҫ����
����Ҫ����������������Ƚ�
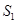 ��
�� ��С
����s1=a2+4a;s2=a2+4a+4 �� s1��s2
�����������1��������֪ͼ2�г����εij�=a+4����=a�����Գ����ε����Ϊ
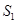 = a2+4a;
= a2+4a;ͼ3�������α߳�Ϊa+2�����
 = a2+4a+4
= a2+4a+4��2�����������֪
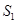 -
- =-4��0.����
=-4��0.����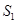 ��
��
�����������Ѷ��еȣ���Ҫ����ѧ��������֪�����еĹ��ɽ�ϲ���ʽ���̽�����������Ϊ�п��������ͣ�ע�����ν��Ӧ�ã��ι����ռ��ɡ�

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ





 ABCD�У�
ABCD�У� Ϊ
Ϊ �е㣬����
�е㣬���� �Ĵ��߽�
�Ĵ��߽� ����
���� ���ӳ����ڵ�
���ӳ����ڵ� ������
������ .��
.�� ��
�� ��
�� ����
���� �ij���
�ij���

 ��
�� �ֱ���ƽ���ı���
�ֱ���ƽ���ı��� �ı�
�ı� ��
�� �ϵ����㣬��
�ϵ����㣬��  ��
��
 ��
�� �Ƿ���ƽ���ı���?
�Ƿ���ƽ���ı���?