题目内容
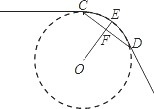
如图,一条公路的转弯处是一段圆弧
,点O是
的圆心,E为
上一点,OE⊥CD,垂足为F.已知CD=600m,EF=100m,求这段弯路的半径.
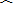 |
| CD |
 |
| CD |
 |
| CD |

连接OC.设这段弯路的半径为R米
则OF=OE-EF=R-100
∵OE⊥CD
∴CF=
CD=
×600=300
根据勾股定理,得OC2=CF2+OF2
即R2=3002+(R-100)2
解之,得R=500
所以这段弯路的半径为500米.
则OF=OE-EF=R-100
∵OE⊥CD
∴CF=
| 1 |
| 2 |
| 1 |
| 2 |
根据勾股定理,得OC2=CF2+OF2
即R2=3002+(R-100)2
解之,得R=500
所以这段弯路的半径为500米.


练习册系列答案
相关题目