题目内容
【题目】在正方形ABCD中,AB=6,M为对角线BD上任意一点(不与B、D重合),连接CM,过点M作MN⊥CM,交AB(或AB的延长线)于点N,连接CN.
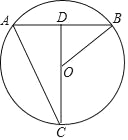
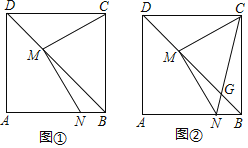
感知:如图①,当M为BD的中点时,易证CM=MN.(不用证明)
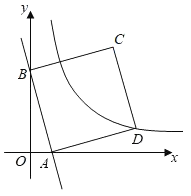
探究:如图②,点M为对角线BD上任一点(不与B、D重合).请探究MN与CM的数量关系,并证明你的结论.
应用:(1)直接写出△MNC的面积S的取值范围 ;
(2)若DM:DB=3:5,则AN与BN的数量关系是 .
【答案】探究:见解析;应用:(1)9≤S<18;(2)AN=6BN.
【解析】
探究:如图①中,过M分别作ME∥AB交BC于E,MF∥BC交AB于F,证明△MFN≌△MEC(ASA)即可解决问题.
应用:(1)求出△MNC面积的最大值以及最小值即可解决问题.
(2)利用平行线分线段成比例定理求出AN,BN即可解决问题.
解:探究:如图①中,过M分别作ME∥AB交BC于E,MF∥BC交AB于F,
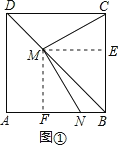
则四边形BEMF是平行四边形,
∵四边形ABCD是正方形,
∴∠ABC=90°,∠ABD=∠CBD=∠BME=45°,
∴ME=BE,
∴平行四边形BEMF是正方形,
∴ME=MF,
∵CM⊥MN,
∴∠CMN=90°,
∵∠FME=90°,
∴∠CME=∠FMN,
∴△MFN≌△MEC(ASA),
∴MN=MC;
应用:(1)当点M与D重合时,△CNM的面积最大,最大值为18,
当DM=BM时,△CNM的面积最小,最小值为9,
综上所述,9≤S<18.
(2)如图②中,
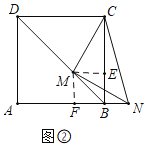
由(1)得FM∥AD,EM∥CD,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∵AN=BC=6,
∴AF=3.6,CE=3.6,
∵△MFN≌△MEC,
∴FN=EC=3.6,
∴AN=7.2,BN=7.2﹣6=1.2,
∴AN=6BN,
故答案为AN=6BN.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案