题目内容
【题目】如图,在△ABC中,∠A=60°,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ,则∠F= . 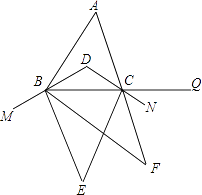
【答案】15°
【解析】解:∵BD、CD分别平分∠ABC、∠ACB,∠A=60°, ∴∠DBC= ![]() ∠ABC,∠DCB=
∠ABC,∠DCB= ![]() ∠ACB,
∠ACB,
∴∠DBC+∠DCB= ![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() (180°﹣∠A)=
(180°﹣∠A)= ![]() ×(180°﹣60°)=60°,
×(180°﹣60°)=60°,
∴∠MBC+∠NCB=360°﹣60°=300°,
∵BE、CE分别平分∠MBC、∠BCN,
∴∠5+∠6= ![]() ∠MBC,∠1=
∠MBC,∠1= ![]() ∠NCB,
∠NCB,
∴∠5+∠6+∠1= ![]() (∠NCB+∠NCB)=150°,
(∠NCB+∠NCB)=150°,
∴∠E=180°﹣(∠5+∠6+∠1)=180°﹣150°=30°,
∵BF、CF分别平分∠EBC、∠ECQ,
∴∠5=∠6,∠2=∠3+∠4,
∵∠3+∠4=∠5+∠F,∠2+∠3+∠4=∠5+∠6+∠E,
即∠2=∠5+∠F,2∠2=2∠5+∠E,
∴2∠F=∠E,
∴∠F= ![]() ∠E=
∠E= ![]() ×30°=15°.
×30°=15°.
故答案为15°.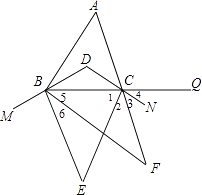
先由BD、CD分别平分∠ABC、∠ACB得到∠DBC= ![]() ∠ABC,∠DCB=
∠ABC,∠DCB= ![]() ∠ACB,在△ABC中根据三角形内角和定理得∠DBC+∠DCB=
∠ACB,在△ABC中根据三角形内角和定理得∠DBC+∠DCB= ![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() (180°﹣∠A)=60°,则根据平角定理得到∠MBC+∠NCB=300°;再由BE、CE分别平分∠MBC、∠BCN得∠5+∠6=
(180°﹣∠A)=60°,则根据平角定理得到∠MBC+∠NCB=300°;再由BE、CE分别平分∠MBC、∠BCN得∠5+∠6= ![]() ∠MBC,∠1=
∠MBC,∠1= ![]() ∠NCB,两式相加得到∠5+∠6+∠1=
∠NCB,两式相加得到∠5+∠6+∠1= ![]() (∠NCB+∠NCB)=150°,在△BCE中,根据三角形内角和定理可计算出∠E=30°;再由BF、CF分别平分∠EBC、∠ECQ得到∠5=∠6,∠2=∠3+∠4,根据三角形外角性质得到∠3+∠4=∠5+∠F,∠2+∠3+∠4=∠5+∠6+∠E,利用等量代换得到∠2=∠5+∠F,2∠2=2∠5+∠E,再进行等量代换可得到∠F=
(∠NCB+∠NCB)=150°,在△BCE中,根据三角形内角和定理可计算出∠E=30°;再由BF、CF分别平分∠EBC、∠ECQ得到∠5=∠6,∠2=∠3+∠4,根据三角形外角性质得到∠3+∠4=∠5+∠F,∠2+∠3+∠4=∠5+∠6+∠E,利用等量代换得到∠2=∠5+∠F,2∠2=2∠5+∠E,再进行等量代换可得到∠F= ![]() ∠E.
∠E.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案